Some circle equivalences
Some circle equivalences
This is a work in progress jointly with Marc Bezem. Some of the following proofs are collapsed or hidden to reduce the size of the document. Nevertheless, the reader can click on them to open the full description. Pictures are also clickable.
In this entry, we want to show some equivalences between the circle and other higher inductive types.
{-# OPTIONS --without-K #-} open import Agda.Primitive using ( Level ; lsuc; lzero; _⊔_ ) open import MiniHoTT hiding (S¹;base;loop;S¹-rec;S¹-βrec;S¹-ind;S¹-βind;neg) module _ where
S¹ type
The circle is the higher inductive type with one point and one no trivial path called path as we can see in the following picture.
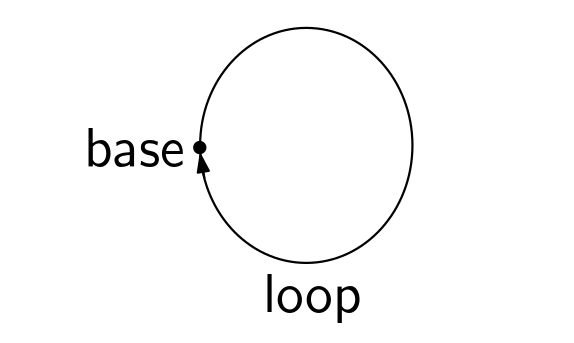 Figure 1. The circle type
Figure 1. The circle type S¹.
Definition
-- Definition of the Circle S¹ using an Agda hack. module _ where private data !S¹ : Type₀ where !base : !S¹ S¹ : Type₀ S¹ = !S¹ base : S¹ base = !base -- Nontrivial path on the circle. postulate loop : base == base
-- Def. loop^2 _² : ∀ {ℓ} {A : Type ℓ} {a : A} → a == a -------- → a == a p ² = p · p
Recursion principle
Recursion principle on points:
-- Def. S¹-rec : ∀ {ℓ} → (A : Type ℓ) → (a : A) → (p : a == a) -------------- → (S¹ → A) S¹-rec A a p !base = a
Recursion on paths:
-- Postulate. postulate S¹-βrec : ∀ {ℓ} → (A : Type ℓ) → (a : A) → (p : a == a) ----------------------------- → ap (S¹-rec A a p) loop == p
Induction principle
Induction principle on points:
-- Def. S¹-ind : ∀ {ℓ} (P : S¹ → Type ℓ) → (x : P base) → (x == x [ P ↓ loop ]) ------------------------ → ((t : S¹) → P t) S¹-ind P x p !base = x
Induction principle on paths:
-- Postulate. postulate S¹-βind : ∀ {ℓ} (P : S¹ → Type ℓ) → (x : P base) → (p : x == x [ P ↓ loop ]) ------------------------------- → apd (S¹-ind P x p) loop == p
pS type
The pS type as the figure below shows, it is a circle with two edges
in opposite direction between two points. Notice this HIT is just different
form the suspension of booleans (Σ 2) by reversing one arrow.
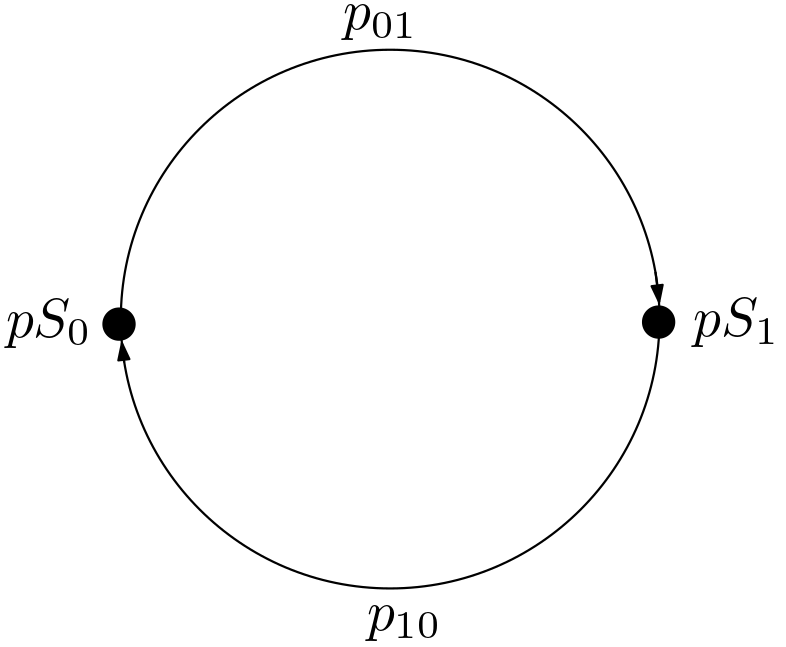 Figure 2.
Figure 2. pS Type.
-- Definition of pS type using an Agda hack. module _ where private data #!pS : Type lzero where #!pS₀ : #!pS #!pS₁ : #!pS data !pS : Type lzero where !ps : #!pS → (Unit → Unit) → !pS pS : Type₀ pS = !pS pS₀ : pS pS₀ = !ps #!pS₀ _ pS₁ : pS pS₁ = !ps #!pS₁ _ postulate p₀₁ : pS₀ == pS₁ p₁₀ : pS₁ == pS₀
Recursion principle
Recursion principle on points:
-- Def. pS-rec : (C : Type₀) → (c₀ c₁ : C) → (p₀₁' : c₀ == c₁) → (p₁₀' : c₁ == c₀) -------------------- → (pS → C) pS-rec C c₀ c₁ p₀₁' p₁₀' (!ps #!pS₀ x₁) = c₀ pS-rec C c₀ c₁ p₀₁' p₁₀' (!ps #!pS₁ x₁) = c₁
Recursion principle on paths:
-- Postulate. postulate pS-βrec₀₁ : (C : Type₀) → (c₀ c₁ : C) → (p₀₁' : c₀ == c₁) → (p₁₀' : c₁ == c₀) ------------------------------------------- → ap (pS-rec C c₀ c₁ p₀₁' p₁₀') p₀₁ == p₀₁' pS-βrec₁₀ : (C : Type₀) → (c₀ c₁ : C) → (p₀₁' : c₀ == c₁) → (p₁₀' : c₁ == c₀) -------------------------------------------- → ap (pS-rec C c₀ c₁ p₀₁' p₁₀') p₁₀ == p₁₀'
Induction principle
Induction principle on points:
-- Def. pS-ind : ∀ {ℓ} (C : pS → Type ℓ) → (c₀ : C pS₀) → (c₁ : C pS₁) → (q₁ : c₀ == c₁ [ C ↓ p₀₁ ]) → (q₂ : c₁ == c₀ [ C ↓ p₁₀ ]) ----------------------------- → ((t : pS) → C t) pS-ind C c₀ c₁ q₁ q₂ (!ps #!pS₀ x₁) = c₀ pS-ind C c₀ c₁ q₁ q₂ (!ps #!pS₁ x₁) = c₁
Induction principle on paths:
-- Postulate. postulate pS-βind₀₁ : ∀ {ℓ} (C : pS → Type ℓ) → (c₀ : C pS₀) → (c₁ : C pS₁) → (p₀₁' : c₀ == c₁ [ C ↓ p₀₁ ]) → (p₁₀' : c₁ == c₀ [ C ↓ p₁₀ ]) → ((t : pS) → C t) -------------------------------------------- → apd (pS-ind C c₀ c₁ p₀₁' p₁₀') p₀₁ == p₀₁' pS-βind₁₀ : ∀ {ℓ} (C : pS → Type ℓ) → (c₀ : C pS₀) → (c₁ : C pS₁) → (p₀₁' : c₀ == c₁ [ C ↓ p₀₁ ]) → (p₁₀' : c₁ == c₀ [ C ↓ p₁₀ ]) → ((t : pS) → C t) ------------------------------------------- → apd (pS-ind C c₀ c₁ p₀₁' p₁₀') p₁₀ == p₁₀'
S¹ ≃ pS
Lemma 1 .
Proof. We proceed as usual. Defining the outgoing functions and proving the homotopies. We prove the equivalence by quasiinverse equivalence.
For this equivalence, we need to find a proper candidate to correspond
with the loop path of S¹. Our propose is p₀₀, the path p₀₁ · p₁₀.
This choice makes sense because
p₀₀ suggests a loop, closing the circuit with the arrows.
p₀₀ : pS₀ == pS₀ p₀₀ = p₀₁ · p₁₀
Outgoing functions
We define the function f that goes from S¹ to pS type.
Which it means we need to use the recursion principle of the circle.
We map base to pS₀ and the action on loop to
(tr (λ p → pS₀ == pS₀) loop p₀₀).
module Lemma₁ where private f : S¹ → pS f = S¹-rec pS pS₀ (tr (λ p → pS₀ == pS₀) loop p₀₀)
For the inverse function of f we have g which goes from pS to S¹. g is
defined by the recursion principle of pS type. The correspondence in this case
maps all the points to base in S¹, and the arrows p₀₁ and p₁₀ to loop ²
and loop ⁻¹ respectively. The reason for these last choices is because their
concatenation gives a loop which is exactly the correspondence that we want to
have. Another possible choices would be if we take instead loop and refl
base but that would give us a different proof and p₀₀ could be something
else.
-- Inverse g : pS → S¹ g = pS-rec S¹ base base (loop ²) (loop ⁻¹)
Now, let’s prove the respective homotopies to show the equivalence.
f ∘ g ~ id
To prove the homotopy , we also need recursion
principle of pS type as it follows.
- Case
pS₁:
-- Def. q₁ : f (g pS₁) == pS₁ q₁ = ! p₀₀ · ! p₀₀ · p₀₁
Case on paths:
-- Def. dpath₀ : refl pS₀ == q₁ [ (λ z → (f ∘ g) z == id z) ↓ p₀₁ ] dpath₀ = begin transport (λ z → (f ∘ g) z == id z) p₀₁ idp ==⟨ transport-eq-fun (f ∘ g) id p₀₁ idp ⟩ ! ap (f ∘ g) p₀₁ · idp · ap id p₀₁ ==⟨ ·-assoc _ idp (ap id p₀₁) ⟩ ! ap (f ∘ g) p₀₁ · (idp · ap id p₀₁) ==⟨ ap (λ r → ! ap (f ∘ g) p₀₁ · r) (·-lunit (ap id p₀₁)) ⟩ ! ap (f ∘ g) p₀₁ · (ap id p₀₁) ==⟨ ap (λ r → ! ap (f ∘ g) p₀₁ · r) (ap-id p₀₁) ⟩ ! ap (f ∘ g) p₀₁ · p₀₁ ==⟨ ap (λ r → ! r · p₀₁) (! (ap-comp g f p₀₁)) ⟩ ! ap f (ap g p₀₁) · p₀₁ ==⟨ ap (λ r → ! ap f r · p₀₁) (pS-βrec₀₁ S¹ base base (loop · loop) idp) ⟩ ! ap f (loop ²) · p₀₁ ==⟨ ap (λ r → ! r · p₀₁) (ap-· f loop loop) ⟩ ! (ap f loop · ap f loop) · p₀₁ ==⟨ ap (λ r → ! (r · ap f loop) · p₀₁) (S¹-βrec pS pS₀ (transport (λ _ → pS₀ == pS₀) loop p₀₀)) ⟩ ! (transport (λ p → pS₀ == pS₀) loop p₀₀ · ap f loop) · p₀₁ ==⟨ ap (λ r → ! (r · ap f loop) · p₀₁) (transport-const loop p₀₀) ⟩ ! (p₀₀ · ap f loop) · p₀₁ ==⟨ ap (λ r → ! (p₀₀ · r) · p₀₁) (S¹-βrec pS pS₀ (transport (λ _ → pS₀ == pS₀) loop p₀₀)) ⟩ ! (p₀₀ · transport (λ p → pS₀ == pS₀) loop p₀₀) · p₀₁ ==⟨ ap (λ r → ! (p₀₀ · r) · p₀₁)(transport-const loop p₀₀) ⟩ ! (p₀₀ · p₀₀) · p₀₁ ==⟨ ap (_· p₀₁) (!-· p₀₀ p₀₀) ⟩ q₁ ∎
-- Def. dpath₁ : q₁ == refl pS₀ [ (λ z → (f ∘ g) z == id z) ↓ p₁₀ ] dpath₁ = begin transport (λ z → (f ∘ g) z == id z) p₁₀ q₁ ==⟨ transport-eq-fun (f ∘ g) id p₁₀ q₁ ⟩ ! ap (f ∘ g) p₁₀ · q₁ · ap id p₁₀ ==⟨ ap (λ r → ! ap (f ∘ g) p₁₀ · q₁ · r) (ap-id p₁₀) ⟩ ! ap (f ∘ g) p₁₀ · q₁ · p₁₀ ==⟨ ap (λ r → ! r · q₁ · p₁₀) (! (ap-comp g f p₁₀)) ⟩ ! ap f (ap g p₁₀) · q₁ · p₁₀ ==⟨ ap (λ r → ! ap f r · q₁ · p₁₀) (pS-βrec₁₀ S¹ base base idp (! loop)) ⟩ ! ap f (! loop) · q₁ · p₁₀ ==⟨ ap (λ r → ! r · q₁ · p₁₀) (ap-inv f loop) ⟩ (! ! ap f loop) · q₁ · p₁₀ ==⟨ ap (λ r → r · q₁ · p₁₀) (involution {p = ap f loop}) ⟩ ap f loop · q₁ · p₁₀ ==⟨ ap (λ r → r · q₁ · p₁₀) (S¹-βrec pS pS₀ (transport (λ _ → pS₀ == pS₀) loop (p₀₁ · p₁₀))) ⟩ (transport (λ p → pS₀ == pS₀) loop p₀₀) · q₁ · p₁₀ ==⟨ ap (λ r → r · q₁ · p₁₀) (transport-const loop p₀₀) ⟩ p₀₀ · q₁ · p₁₀ ==⟨ idp ⟩ p₀₀ · (! p₀₀ · ! p₀₀ · p₀₁) · p₁₀ ==⟨ ap (λ r → p₀₀ · r · p₁₀) (·-assoc (! p₀₀) (! p₀₀) p₀₁) ⟩ p₀₀ · (! p₀₀ · (! p₀₀ · p₀₁)) · p₁₀ ==⟨ ap (λ r → r · p₁₀) (! (·-assoc p₀₀ (! p₀₀) (! p₀₀ · p₀₁))) ⟩ (p₀₀ · ! p₀₀ ) · (! p₀₀ · p₀₁) · p₁₀ ==⟨ ap (λ r → r · (! p₀₀ · p₀₁) · p₁₀) (·-rinv p₀₀) ⟩ idp · (! p₀₀ · p₀₁) · p₁₀ ==⟨ ap (_· p₁₀) ( ! ·-lunit ((! p₀₀ · p₀₁))) ⟩ (! p₀₀ · p₀₁) · p₁₀ ==⟨ ·-assoc (! p₀₀) p₀₁ p₁₀ ⟩ ! p₀₀ · (p₀₁ · p₁₀) ==⟨⟩ ! p₀₀ · p₀₀ ==⟨ ·-linv p₀₀ ⟩ idp ==⟨⟩ refl pS₀ ∎
Finally, by path induction on pS type, we got the homotopy.
-- Homotopy. H₁ : f ∘ g ∼ id H₁ = pS-ind _ (refl pS₀) q₁ dpath₀ dpath₁
g ∘ f ~ id
To prove the homotopy , we proceed by induction on
the circle. For the base case, refl base works since g (f base) is
definitionally equal to base.
-- Def. H₂-base : g (f base) == base H₂-base = refl base
Action on loop case:
-- Def. H₂-loop : refl base == refl base [ (λ z → (g ∘ f) z == id z) ↓ loop ] H₂-loop = (begin transport (λ z → (g ∘ f) z == id z) loop idp ==⟨ transport-eq-fun (g ∘ f) id loop idp ⟩ ! (ap (g ∘ f) loop) · idp · ap id loop ==⟨ ap (λ r → ! (ap (g ∘ f) loop) · idp · r) (ap-id loop) ⟩ ! (ap (g ∘ f) loop) · idp · loop ==⟨ ·-assoc _ idp loop ⟩ ! (ap (g ∘ f) loop) · (idp · loop) ==⟨ ap (λ r → ! (ap (g ∘ f) loop) · r) (·-lunit loop) ⟩ ! (ap (g ∘ f) loop) · loop ==⟨ ap (λ r → ! r · loop) (! (ap-comp f g loop)) ⟩ ! ap g (ap f loop) · loop ==⟨ ap {A = pS₀ == pS₀} (λ r → ( ! (ap g r)) · loop) (S¹-βrec pS pS₀ _) ⟩ ! ap g (transport (λ p → pS₀ == pS₀) loop p₀₀) · loop ==⟨ ap {A = pS₀ == pS₀} (λ r → ! ap g r · loop) (transport-const loop p₀₀) ⟩ ! ap g p₀₀ · loop ==⟨ ap (λ r → ! r · loop) (ap-· g p₀₁ p₁₀) ⟩ ! (ap g p₀₁ · ap g p₁₀) · loop ==⟨ ap {A = base == base} (λ r → ! (r · ap g p₁₀) · loop) (pS-βrec₀₁ S¹ base base (loop · loop) idp) ⟩ ! ((loop ²) · ap g p₁₀) · loop ==⟨ ap {A = base == base} (λ r → ! ( loop · loop · r) · loop) (pS-βrec₁₀ S¹ base base idp (inv loop)) ⟩ ! ((loop ²) · ! loop) · loop ==⟨ ap (λ r → ! r · loop) aux-path ⟩ ! loop · loop ==⟨ ·-linv loop ⟩ idp ∎) where aux-path : (loop ²) · (loop ⁻¹) == loop aux-path = begin (loop ²) · (loop ⁻¹) ==⟨ ·-assoc loop loop (! loop) ⟩ loop · (loop · ! loop) ==⟨ ap (loop ·_) (·-rinv loop) ⟩ loop · idp ==⟨ ! (·-runit loop) ⟩ loop ∎
-- Homotopy H₂ : g ∘ f ∼ id H₂ = S¹-ind _ H₂-base H₂-loop
Now, everything we needed to prove the equivalence is and the equivalence is by quasiinverse equivalence.
-- Equivalence. S¹-≃-pS : S¹ ≃ pS S¹-≃-pS = qinv-≃ f (g , H₁ , H₂)
Σ S¹ P ≃ pS
Lemma 3. where and .
P is a type family defined by the recursion principle of the circle.
When it is the base case, P base is definitionally equal to the booleans Bool.
When P is acting on loop, a path of type Bool == Bool is given
by Univalence Axiom and the equivalence neg, the negation function for booleans.
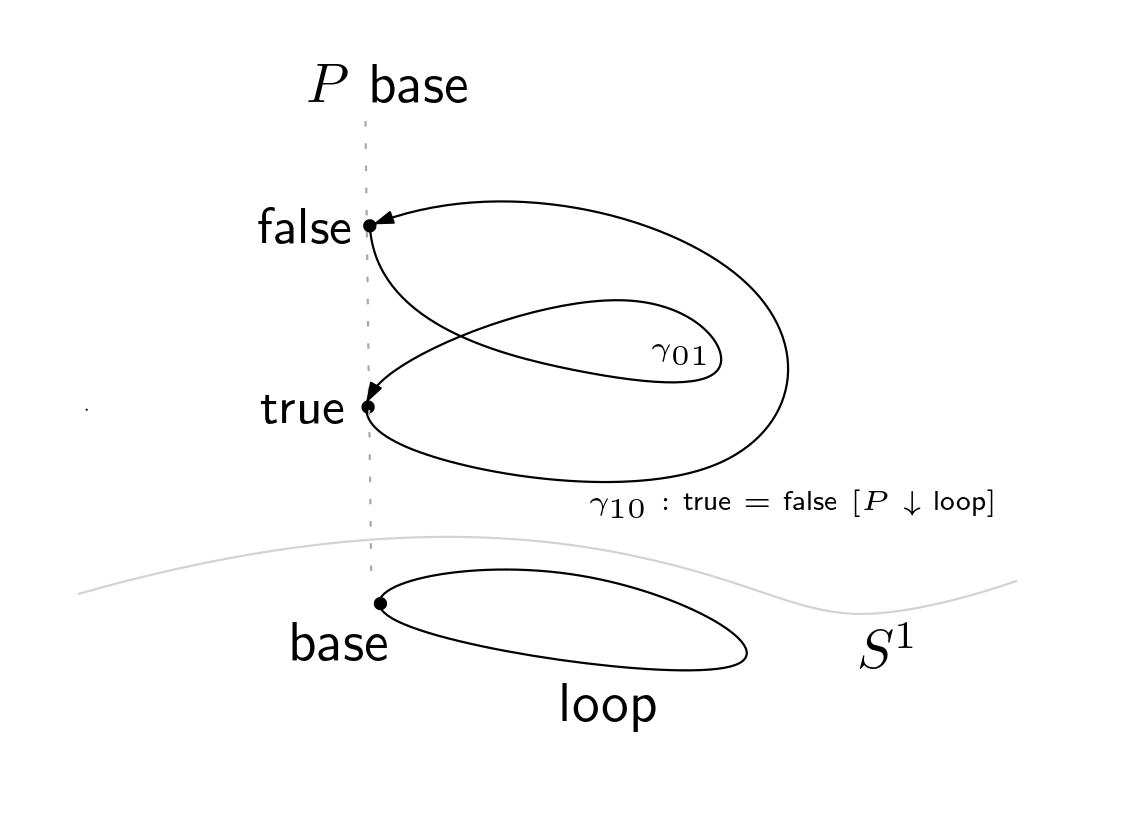 Figure 3.
Figure 3. P type family.
Let’s define this type family formally.
module Lemma₃ where -- Def. neg : Bool → Bool neg true = false neg false = true -- Equiv. neg-eq : Bool ≃ Bool neg-eq = qinv-≃ neg (neg , h , h) where h : neg ∘ neg ∼ id h true = idp h false = idp
The type family P : S¹ → Type₀.
-- Def P : S¹ → Type₀ P = S¹-rec Type₀ Bool (ua neg-eq)
As we saw in the Fig. 3, the paths γ₀₁ and γ₁₀ are defined as pathovers.
-- Defs. γ₀₁ : tr P loop false == true γ₀₁ = transport-ua P loop neg-eq (S¹-βrec Type₀ Bool (ua neg-eq)) false γ₁₀ : tr P loop true == false γ₁₀ = transport-ua P loop neg-eq (S¹-βrec Type₀ Bool (ua neg-eq)) true
Proof. We proceed as usual to show the equivalence.
We define the outgoing functions f : Σ S¹ P → pS, g : pS → Σ S¹ P
and the homotopies f ∘ g ~ id and g ∘ f ∼ id. Let’s start defining
the function f.
f : Σ S¹ P → pS
To define f we need to use the recursor principle of Sigma types which gives a
pair (b , x) in order to provide a definition for the uncurried version of
f, f̰ : (b : S¹) → P b → pS. Since f̰ is a dependent function, we define
it using induction principle on the circle. In this case, we maps base to ct
and p̰ as evidence of the pathover of ct and ct along the loop in the
family (λ z → P z → pS).
-- Def. ct : P base → pS ct true = pS₁ ct false = pS₀
-- Def. p̰ : ct == ct [ (λ z → P z → pS) ↓ loop ] p̰ = (begin transport (λ z → P z → pS) loop ct ==⟨ transport-fun loop ct ⟩ ff ==⟨ funext (λ x → (ff-gg' x) · (gg-hh' x)) ⟩ hh ==⟨ funext helper₂ ⟩ ct ∎) where open import UnivalenceLemmas helper₁ : (x : P base) → x == neg x [ P ↓ ! loop ] helper₁ x = let apP!loop : ap P (! loop) == ua (invEqv neg-eq) apP!loop = begin ap P (! loop) ==⟨ ap-inv P loop ⟩ ! ap P loop ==⟨ ap (!_) (S¹-βrec Type₀ Bool (ua (neg-eq))) ⟩ ! ua (neg-eq) ==⟨ ! (UnivalenceLemmas.ua-inv neg-eq) ⟩ ua (invEqv neg-eq) ∎ in begin transport P (! loop) x ==⟨ transport-ua P (! loop) (invEqv neg-eq) apP!loop x ⟩ fun≃ (invEqv (neg-eq)) x ==⟨⟩ fun≃ (neg-eq) x ==⟨⟩ neg x ∎ helper₂ : (x : P base) → ct (neg x) == ct x helper₂ true = p₀₁ helper₂ false = p₁₀ ff : (x : P base) → pS ff = (λ (x : P base) → transport (λ z → pS) loop (ct (transport (λ z → P z) (! loop) x))) gg : (x : P base) → pS gg = (λ (x : P base) → (ct (transport (λ z → P z) (! loop) x))) ff-gg' : (x : P base) → ff x == gg x ff-gg' = (λ (pb : P base) → transport-const loop (ct (transport (λ z → P z) (! loop) pb))) ff-gg : ff == gg ff-gg = funext ff-gg' hh : (x : P base) → pS hh = λ (x : P base) → ct (neg x) gg-hh' : (x : P base) → gg x == hh x gg-hh' = (λ (pb : P base) → ap ct (helper₁ pb)) gg-hh : gg == hh gg-hh = funext gg-hh'
-- Def. f̰ : (b : S¹) → P b → pS f̰ = S¹-ind (λ z → P z → pS) ct p̰
-- Def. f : Σ S¹ P → pS f (b , x) = f̰ b x
g : pS → Σ S¹ P
We define g as the inverse function of f by recursion on pS type. Since
pS and Σ S¹ P both have two points, two arrows and their graphs are actually
isomorphic, g entitled such a correspond as it is expected. false maps to
(base , false), true maps to (base, true). For the paths, the subindexes will suggest
the correspondence: p₀₁ maps to (base , false) == (base , true ), and p₁₀ maps to
(base , true) == (base, false). For these last paths, we use
Theorem 2.9.7 in (Univalent Foundations Program, 2013) to get the respective dependent pair equalities, this is
by using the pair= function.
-- Def. ctp : P base → Σ S¹ P ctp b = base , b ptp : (y : P base) → ctp y == ctp (neg y) ptp false = pair= (loop , γ₀₁) ptp true = pair= (loop , γ₁₀) g : pS → Σ S¹ P g = pS-rec (Σ S¹ P) (ctp false) -- false ↦ (base , false) (ctp true) -- true ↦ (base , true) (ptp false) -- p₀₁ ↦ (base , false) = (base , true) (ptp true) -- p₁₀ ↦ (base , true ) = (base , false)
f ∘ g ∼ id
To show that this homotopy holds, we proceed by induction principle of pS
type. This means we need to show the identity types (f ∘ g) pS₀ == id pS₀ and
(f ∘ g) pS₁ == id pS₁ are inhabited but also the pathovers along p₀₁ and
p₁₀ respectively. These are the terms q₀, q₁, pover₁, and pover₂ in
the following. To define pover₁ and pover₂ we need the following lemmas
based on Lemma 6.12.8 in (missing reference) and postulated here because of its
complexity.
-- Lemma 6.12.8 -- postulate -- lemma-ap-f-γ₀₁ : ap f (ptp false) == p₀₁ -- lemma-ap-f-γ₁₀ : ap f (ptp true) == p₁₀
-- Def. -- q₀ : (f ∘ g) pS₀ == id pS₀ -- q₀ = p₀₁ · p₁₀
-- Def. -- q₁ : (f ∘ g) pS₁ == id pS₁ -- q₁ = p₁₀ · p₀₁
-- Def. -- pover₁ : q₀ == q₁ [ (λ z → (f ∘ g) z == id z) ↓ p₀₁ ] -- pover₁ = -- (begin -- transport (λ z → (f ∘ g) z == id z) p₀₁ q₀ -- ==⟨ transport-eq-fun (f ∘ g) id p₀₁ q₀ ⟩ -- ! ap (f ∘ g) p₀₁ · q₀ · ap id p₀₁ -- ==⟨ ap (! ap (f ∘ g) p₀₁ · q₀ ·_) (ap-id p₀₁) ⟩ -- ! ap (f ∘ g) p₀₁ · q₀ · p₀₁ -- ==⟨ ap (λ r → ! r · q₀ · p₀₁) (! ap-comp g f p₀₁) ⟩ -- ! ap f (ap g p₀₁) · q₀ · p₀₁ -- ==⟨ ap (λ r → ! ap f r · q₀ · p₀₁) (pS-βrec₀₁ (Σ S¹ (λ b → P b)) (ctp false) (ctp true) (ptp false) (ptp true)) ⟩ -- ! ap f (ptp false) · q₀ · p₀₁ -- ==⟨ ap (λ r → ! r · q₀ · p₀₁) lemma-ap-f-γ₀₁ ⟩ -- ! p₀₁ · q₀ · p₀₁ -- ==⟨ idp ⟩ -- ! p₀₁ · (p₀₁ · p₁₀) · p₀₁ -- ==⟨ ! (·-assoc (! p₀₁) p₀₁ p₁₀) |in-ctx (_· p₀₁) ⟩ -- (! p₀₁ · p₀₁) · p₁₀ · p₀₁ -- ==⟨ ·-linv p₀₁ |in-ctx (λ r → r · p₁₀ · p₀₁) ⟩ -- idp · p₁₀ · p₀₁ -- ==⟨⟩ -- q₁ -- ∎)
-- Def. -- pover₂ : q₁ == q₀ [ (λ z → (f ∘ g) z == id z) ↓ p₁₀ ] -- -- pover₂ = -- (begin -- transport (λ z → (f ∘ g) z == id z) p₁₀ q₁ -- ==⟨ transport-eq-fun (f ∘ g) id p₁₀ q₁ ⟩ -- ! ap (f ∘ g) p₁₀ · q₁ · ap id p₁₀ -- ==⟨ ap (! ap (f ∘ g) p₁₀ · q₁ ·_) (ap-id p₁₀) ⟩ -- ! ap (f ∘ g) p₁₀ · q₁ · p₁₀ -- ==⟨ ap (λ r → ! r · q₁ · p₁₀) (! ap-comp g f p₁₀) ⟩ -- ! ap f (ap g p₁₀) · q₁ · p₁₀ -- ==⟨ ap (λ r → ! ap f r · q₁ · p₁₀) -- (pS-βrec₁₀ (Σ S¹ (λ b → P b)) (ctp false) (ctp true) (ptp false) (ptp true)) ⟩ -- ! ap f (ptp true) · q₁ · p₁₀ -- ==⟨ ap (λ r → ! r · q₁ · p₁₀) lemma-ap-f-γ₁₀ ⟩ -- ! p₁₀ · q₁ · p₁₀ -- ==⟨⟩ -- ! p₁₀ · (p₁₀ · p₀₁) · p₁₀ -- ==⟨ ! (·-assoc (! p₁₀) p₁₀ p₀₁) |in-ctx (_· p₁₀) ⟩ -- (! p₁₀ · p₁₀) · p₀₁ · p₁₀ -- ==⟨ ·-linv p₁₀ |in-ctx (λ r → r · p₀₁ · p₁₀) ⟩ -- idp · p₀₁ · p₁₀ -- ==⟨⟩ -- q₀ -- ∎)
Finally, our homotopy holds:
-- Homotopy -- f-g : f ∘ g ∼ id -- f-g = pS-ind (λ ps → (f ∘ g) ps == id ps) q₀ q₁ pover₁ pover₂
g ∘ f ∼ id
This homotopy is a very more complex. To show that for all x : S¹ it holds g
(f x) == id x we must proceed by induction three times. We perform this in the
following order: Sigma induction, Circle induction and pS induction.
Since the last two cases are induction on HITs, these inductions take into account the action on their path constructors. We have taken inspiration to finish this proof from Flattening lemma’s proof in Section 6 in (Univalent Foundations Program, 2013).
By Sigma induction, we must to provide the uncurried function g-f' of g-f : g
∘ f ∼ id, that has type Π (s : S¹) Π (b : P s).(g ∘ f) (s , b) == id (s , b).
Therefore, the next step is by induction on the circle. For the base case we
have c defined as fallows. For acting on paths, we define a short name Q for
the type family λ z → (b : P z) → (g ∘ f) (z , b) == id (z , b) in order to
get a pathover between c and itself along loop in the type family Q, this
path is cpath. To define cpath we require a few auxiliary lemmas that
an interested reader can make them explicit by clicking on the helpers section
below. The equivalence follows by showing that f defines a quasiinverse
equivalence (ΣS¹P-≃-pS).
-- Def. -- c : (b : P base) → (g ∘ f) (base , b) == id (base , b) -- c true = refl (base , true) -- c false = refl (base , false)
-- Def. -- Q : (s : S¹) → Type lzero -- Q = λ z → (b : P z) → (g ∘ f) (z , b) == id (z , b)
-- Helpers and auxiliar lemmas -- Def. -- auxAP : ∀ {x y : P base}{p : base == base} -- → (q : tr (λ x → P x) p x == y) -- → ap (λ w → ctp w ) q == pair= (refl base , q) -- -- auxAP idp = idp -- -- stepFalse1 -- : ∀ {x y : P base} -- → (q : tr (λ x → P x) loop x == y) -- → pair= (loop , refl (tr (λ z → P z) loop x)) · pair= (refl base , q) == pair= (loop , q) -- -- stepFalse1 {x = x} idp = -- begin -- pair= (loop , refl (tr (λ z → P z) loop x)) · pair= (refl base , idp) -- ==⟨ idp ⟩ -- pair= (loop , refl (tr (λ z → P z) loop x)) · idp -- ==⟨ ! ·-runit (pair= (loop , refl (tr P loop x))) ⟩ -- pair= (loop , refl (tr (λ z → P z) loop x)) -- ==⟨ idp ⟩ -- pair= (loop , idp) -- ∎ -- -- stepFalse2 -- : c (tr (λ x → P x) loop false) -- == tr (λ w → (g ∘ f) w == id w) (ap (λ x → ctp x) (! γ₀₁)) (c (neg false)) -- -- stepFalse2 = begin -- c (tr (λ x → P x) loop false) -- ==⟨ ! (apd (λ x → c x) (! γ₀₁)) ⟩ -- tr (λ b → (g ∘ f) (base , b) == id (base , b)) (! γ₀₁) (c (neg false)) -- ==⟨ transport-family (! γ₀₁) (c (neg false)) ⟩ -- tr (λ w → (g ∘ f) w == id w) (ap (λ x → ctp x) (! γ₀₁)) (c (neg false)) -- ∎ -- -- -- -- Def. -- p : (b : P base) → tr (λ w → (g ∘ f) w == id w) (ptp b) (c b) == c (neg b) -- -- p true = -- begin -- tr (λ w → (g ∘ f) w == id w) (ptp true) (c true) -- ==⟨ idp ⟩ -- tr (λ w → (g ∘ f) w == id w) (pair= (loop , γ₁₀)) idp -- ==⟨ transport-eq-fun (g ∘ f) id (pair= (loop , γ₁₀)) idp ⟩ -- ! ap (g ∘ f) (pair= (loop , γ₁₀)) · idp · ap id (pair= (loop , γ₁₀)) -- ==⟨ ap (λ r → ! (ap (g ∘ f) (pair= (loop , γ₁₀))) · idp · r) (ap-id (pair= (loop , γ₁₀))) ⟩ -- ! ap (g ∘ f) (pair= (loop , γ₁₀)) · idp · (pair= (loop , γ₁₀)) -- ==⟨ ap (λ r → r · pair= (loop , γ₁₀)) (! (·-runit (! ap (g ∘ f) (pair= (loop , γ₁₀))))) ⟩ -- ! ap (g ∘ f) (pair= (loop , γ₁₀)) · (pair= (loop , γ₁₀)) -- ==⟨ ap (λ r → ! r · pair= (loop , γ₁₀)) (! ap-comp f g (pair= (loop , γ₁₀))) ⟩ -- ! ap g (ap f (pair= (loop , γ₁₀))) · (pair= (loop , γ₁₀)) -- ==⟨ ap (λ r → ! ap g r · pair= (loop , γ₁₀)) lemma-ap-f-γ₁₀ ⟩ -- ! ap g p₁₀ · (pair= (loop , γ₁₀)) -- ==⟨ ap (λ r → ! r · pair= (loop , γ₁₀)) (pS-βrec₁₀ (Σ S¹ P) (base , false) (base , true) (ptp false) (ptp true)) ⟩ -- ! (ptp true) · (pair= (loop , γ₁₀)) -- ==⟨ idp ⟩ -- ! (pair= (loop , γ₁₀)) · (pair= (loop , γ₁₀)) -- ==⟨ ·-linv (pair= (loop , γ₁₀)) ⟩ -- idp -- ∎ -- -- p false = -- begin -- tr (λ w → (g ∘ f) w == id w) (ptp false) (c false) -- ==⟨ idp ⟩ -- tr (λ w → (g ∘ f) w == id w) (pair= (loop , γ₀₁)) idp -- ==⟨ transport-eq-fun (g ∘ f) id (pair= (loop , γ₀₁)) idp ⟩ -- ! ap (g ∘ f) (pair= (loop , γ₀₁)) · idp · ap id (pair= (loop , γ₀₁)) -- ==⟨ ap (λ r → ! (ap (g ∘ f) (pair= (loop , γ₀₁))) · idp · r) (ap-id (pair= (loop , γ₀₁))) ⟩ -- ! ap (g ∘ f) (pair= (loop , γ₀₁)) · idp · (pair= (loop , γ₀₁)) -- ==⟨ ap (λ r → r · pair= (loop , γ₀₁)) (! (·-runit (! ap (g ∘ f) (pair= (loop , γ₀₁))))) ⟩ -- ! ap (g ∘ f) (pair= (loop , γ₀₁)) · (pair= (loop , γ₀₁)) -- ==⟨ ap (λ r → ! r · pair= (loop , γ₀₁)) (! ap-comp f g (pair= (loop , γ₀₁))) ⟩ -- ! ap g (ap f (pair= (loop , γ₀₁))) · (pair= (loop , γ₀₁)) -- ==⟨ ap (λ r → ! ap g r · pair= (loop , γ₀₁)) lemma-ap-f-γ₀₁ ⟩ -- ! ap g p₀₁ · (pair= (loop , γ₀₁)) -- ==⟨ ap (λ r → ! r · pair= (loop , γ₀₁)) (pS-βrec₀₁ (Σ S¹ P) (base , false) (base , true) (ptp false) (ptp true)) ⟩ -- ! (ptp false) · (pair= (loop , γ₀₁)) -- ==⟨ idp ⟩ -- ! (pair= (loop , γ₀₁)) · (pair= (loop , γ₀₁)) -- ==⟨ ·-linv (pair= (loop , γ₀₁)) ⟩ -- idp -- ∎ -- ------------------------------------------------------------------------------ -- -- -- Def. -- stepFalse3 : -- tr (λ w → (g ∘ f) w == id w) -- ((pair= (loop , refl (tr (λ z → P z) loop false))) · ap (λ x → ctp x) γ₀₁ ) -- (c false) == c (neg false) -- -- stepFalse3 = -- begin -- tr (λ w → (g ∘ f) w == id w) -- ( (pair= (loop , refl (tr (λ z → P z) loop false))) -- · ap (λ x → ctp x) γ₀₁ -- ) -- (c false) -- ==⟨ ap (λ r → tr (λ w → (g ∘ f) w == id w) ((pair= (loop , refl (tr (λ z → P z) loop false))) · r ) (c false)) (auxAP {p = loop} γ₀₁) ⟩ -- tr (λ w → (g ∘ f) w == id w) -- ((pair= (loop , refl (tr (λ z → P z) loop false))) -- · pair= (refl base , γ₀₁)) -- (c false) -- ==⟨ ap (λ r → tr (λ w → (g ∘ f) w == id w) r (c false)) (stepFalse1 γ₀₁) ⟩ -- tr (λ w → (g ∘ f) w == id w) -- (pair= (loop , γ₀₁)) -- (c false) -- ==⟨ p false ⟩ -- c (neg false) -- ∎ -- -- -- Def. -- stepFalse4 : -- tr (λ w → (g ∘ f) w == id w) -- (pair= (loop , refl (tr (λ z → P z) loop false)) · (ap (λ x → ctp x) (γ₀₁)) ) (c false) -- == c (neg false) -- → -- tr (λ w → (g ∘ f) w == id w) -- (pair= (loop , refl (tr (λ z → P z) loop false))) (c false) -- == tr (λ w → (g ∘ f) w == id w) (ap (λ x → ctp x) (! γ₀₁)) (c (neg false)) -- -- stepFalse4 p = -- begin -- tr (λ w → (g ∘ f) w == id w) (pair= (loop , refl (tr (λ z → P z) loop false))) (c false) -- ==⟨ ap (λ r → tr (λ w → (g ∘ f) w == id w) r (c false)) (·-runit (pair= (loop , refl (tr (λ z → P z) loop false)))) ⟩ -- tr (λ w → (g ∘ f) w == id w) (pair= (loop , refl (tr (λ z → P z) loop false)) · idp) (c false) -- ==⟨ ap (λ r → tr (λ w → (g ∘ f) w == id w) (pair= (loop , refl (tr (λ z → P z) loop false)) · r) (c false)) (! (·-rinv (ap (λ x → ctp x) (γ₀₁)))) ⟩ -- tr (λ w → (g ∘ f) w == id w) (pair= (loop , refl (tr (λ z → P z) loop false)) · ((ap (λ x → ctp x) (γ₀₁)) · ! (ap (λ x → ctp x) (γ₀₁)))) (c false) -- ==⟨ ap (λ r → tr (λ w → (g ∘ f) w == id w) r (c false)) (! ·-assoc (pair= (loop , refl (tr (λ z → P z) loop false))) ((ap (λ x → ctp x) (γ₀₁))) (! (ap (λ x → ctp x) (γ₀₁)))) ⟩ -- tr (λ w → (g ∘ f) w == id w) ( (pair= (loop , refl (tr (λ z → P z) loop false)) · ((ap (λ x → ctp x) (γ₀₁))) · ! (ap (λ x → ctp x) (γ₀₁)))) (c false) -- ==⟨ ! (transport-comp-h (pair= (loop , refl (tr (λ z → P z) loop false)) · ap (λ x → ctp x) γ₀₁) (! (ap (λ x → ctp x) (γ₀₁))) (c false)) ⟩ -- tr (λ w → (g ∘ f) w == id w) (! (ap (λ x → ctp x) (γ₀₁))) (tr (λ w → (g ∘ f) w == id w) (pair= (loop , refl (tr (λ z → P z) loop false)) · ((ap (λ x → ctp x) (γ₀₁)))) (c false)) -- ==⟨ ap (λ r → tr (λ w → (g ∘ f) w == id w) (! (ap (λ x → ctp x) (γ₀₁))) r) p ⟩ -- tr (λ w → (g ∘ f) w == id w) (! (ap (λ x → ctp x) (γ₀₁))) (c (neg false)) -- ==⟨ ap (λ r → tr (λ w → (g ∘ f) w == id w) r (c (neg false))) (! ap-inv (λ x → ctp x) γ₀₁) ⟩ -- tr (λ w → (g ∘ f) w == id w) (ap (λ x → ctp x) (! γ₀₁) ) (c (neg false)) -- ∎ -- -- -- Def. -- stepFalse5 : -- tr (λ w → (g ∘ f) w == id w) (pair= (loop , refl (tr (λ z → P z) loop false))) (c false) -- == tr (λ w → (g ∘ f) w == id w) (ap (λ x → ctp x) (! γ₀₁)) (c (neg false)) -- -- stepFalse5 = stepFalse4 stepFalse3 -- -- -- Def. -- stepTrue1 -- : ∀ {x y : P base} -- → (q : tr P loop x == y) -- → pair= (loop , refl (tr P loop x)) · pair= (refl base , q) == pair= (loop , q) -- -- stepTrue1 {x = x} idp = -- begin -- pair= (loop , refl (tr P loop x)) · pair= (refl base , idp) -- ==⟨ idp ⟩ -- pair= (loop , refl (tr P loop x)) · idp -- ==⟨ ! ·-runit (pair= (loop , refl (tr P loop x))) ⟩ -- pair= (loop , refl (tr P loop x)) -- ==⟨ idp ⟩ -- pair= (loop , idp) -- ∎ -- -- -- Def. -- stepTrue2 -- : c (tr (λ x → P x) loop true) -- == tr (λ w → (g ∘ f) w == id w) (ap (λ x → ctp x) (! γ₁₀)) (c (neg true)) -- -- stepTrue2 = begin -- c (tr (λ x → P x) loop true) -- ==⟨ ! (apd (λ x → c x) (! γ₁₀)) ⟩ -- tr (λ b → (g ∘ f) (base , b) == id (base , b)) (! γ₁₀) (c (neg true)) -- ==⟨ transport-family (! γ₁₀) (c (neg true)) ⟩ -- tr (λ w → (g ∘ f) w == id w) (ap (λ x → ctp x) (! γ₁₀)) (c (neg true)) -- ∎ -- -- -- Def. -- stepTrue3 -- : tr (λ w → (g ∘ f) w == id w) -- ((pair= (loop , refl (tr (λ z → P z) loop true))) · ap (λ x → ctp x) γ₁₀ ) -- (c true) == c (neg true) -- -- stepTrue3 = -- begin -- tr (λ w → (g ∘ f) w == id w) -- ( (pair= (loop , refl (tr (λ z → P z) loop true))) -- · ap (λ x → ctp x) γ₁₀ -- ) -- (c true) -- ==⟨ ap (λ r → tr (λ w → (g ∘ f) w == id w) ( (pair= (loop , refl (tr (λ z → P z) loop true))) · r ) (c true)) (auxAP {p = loop} γ₁₀) ⟩ -- tr (λ w → (g ∘ f) w == id w) -- ((pair= (loop , refl (tr (λ z → P z) loop true))) -- · pair= (refl base , γ₁₀)) -- (c true) -- ==⟨ ap (λ r → tr (λ w → (g ∘ f) w == id w) r (c true)) (stepTrue1 γ₁₀) ⟩ -- tr (λ w → (g ∘ f) w == id w) -- (pair= (loop , γ₁₀)) -- (c true) -- ==⟨ p true ⟩ -- c (neg true) -- ∎ -- -- -- Def. -- stepTrue4 : -- tr (λ w → (g ∘ f) w == id w) -- (pair= (loop , refl (tr (λ z → P z) loop true)) · (ap (λ x → ctp x) (γ₁₀)) ) (c true) -- == c (neg true) -- → -- tr (λ w → (g ∘ f) w == id w) -- (pair= (loop , refl (tr (λ z → P z) loop true))) (c true) -- == tr (λ w → (g ∘ f) w == id w) (ap (λ x → ctp x) (! γ₁₀)) (c (neg true)) -- -- stepTrue4 p = -- begin -- tr (λ w → (g ∘ f) w == id w) (pair= (loop , refl (tr (λ z → P z) loop true))) (c true) -- ==⟨ ap (λ r → tr (λ w → (g ∘ f) w == id w) r (c true)) (·-runit (pair= (loop , refl (tr (λ z → P z) loop true)))) ⟩ -- tr (λ w → (g ∘ f) w == id w) (pair= (loop , refl (tr (λ z → P z) loop true)) · idp) (c true) -- ==⟨ ap (λ r → tr (λ w → (g ∘ f) w == id w) (pair= (loop , refl (tr (λ z → P z) loop true)) · r) (c true)) (! (·-rinv (ap (λ x → ctp x) (γ₁₀)))) ⟩ -- tr (λ w → (g ∘ f) w == id w) (pair= (loop , refl (tr (λ z → P z) loop true)) · ((ap (λ x → ctp x) (γ₁₀)) · ! (ap (λ x → ctp x) (γ₁₀)))) (c true) -- ==⟨ ap (λ r → tr (λ w → (g ∘ f) w == id w) r (c true)) (! ·-assoc (pair= (loop , refl (tr (λ z → P z) loop true))) ((ap (λ x → ctp x) (γ₁₀))) (! (ap (λ x → ctp x) (γ₁₀)))) ⟩ -- tr (λ w → (g ∘ f) w == id w) ( (pair= (loop , refl (tr (λ z → P z) loop true)) · ((ap (λ x → ctp x) (γ₁₀))) · ! (ap (λ x → ctp x) (γ₁₀)))) (c true) -- ==⟨ ! (transport-comp-h (pair= (loop , refl (tr (λ z → P z) loop true)) · ap (λ x → ctp x) γ₁₀) (! (ap (λ x → ctp x) (γ₁₀))) (c true)) ⟩ -- tr (λ w → (g ∘ f) w == id w) (! (ap (λ x → ctp x) (γ₁₀))) (tr (λ w → (g ∘ f) w == id w) (pair= (loop , refl (tr (λ z → P z) loop true)) · ((ap (λ x → ctp x) (γ₁₀)))) (c true)) -- ==⟨ ap (λ r → tr (λ w → (g ∘ f) w == id w) (! (ap (λ x → ctp x) (γ₁₀))) r) p ⟩ -- tr (λ w → (g ∘ f) w == id w) (! (ap (λ x → ctp x) (γ₁₀))) (c (neg true)) -- ==⟨ ap (λ r → tr (λ w → (g ∘ f) w == id w) r (c (neg true))) (! ap-inv (λ x → ctp x) γ₁₀) ⟩ -- tr (λ w → (g ∘ f) w == id w) (ap (λ x → ctp x) (! γ₁₀)) (c (neg true)) -- ∎ -- -- -- Def. -- stepTrue5 -- : tr (λ w → (g ∘ f) w == id w) (pair= (loop , refl (tr (λ z → P z) loop true))) (c true) -- == tr (λ w → (g ∘ f) w == id w) (ap (λ x → ctp x) (! γ₁₀)) (c (neg true)) -- -- stepTrue5 = stepTrue4 stepTrue3 -- -- -- Def. -- helper -- : (b : P base) -- → tr (λ w → (g ∘ f) w == id w) (pair= (loop , refl (tr (λ z → P z) loop b))) -- (c b) == c (tr (λ x → P x) loop b) -- -- helper false = -- begin -- tr (λ w → (g ∘ f) w == id w) (pair= (loop , refl (tr (λ z → P z) loop false))) (c false) -- ==⟨ stepFalse5 ⟩ -- tr (λ w → (g ∘ f) w == id w) (ap (λ x → ctp x) (! γ₀₁)) (c (neg false)) -- ==⟨ ! stepFalse2 ⟩ -- c (tr (λ x → P x) loop false) -- ∎ -- -- helper true = -- begin -- tr (λ w → (g ∘ f) w == id w) (pair= (loop , refl (tr (λ z → P z) loop true))) (c true) -- ==⟨ stepTrue5 ⟩ -- tr (λ w → (g ∘ f) w == id w) (ap (λ x → ctp x) (! γ₁₀)) (c (neg true)) -- ==⟨ ! stepTrue2 ⟩ -- c (tr (λ x → P x) loop true) -- ∎
-- Def. -- cpath : PathOver (λ s → (b : P s) → g (f (s , b)) == s , b) loop c c -- cpath = funext-transport-dfun-r loop c c helper
And the homotopy is as follows:
-- Homotopy -- Def. by Sigma induction. Step 1. -- g-f : g ∘ f ∼ id -- g-f (s , b) = g-f' s b -- where -- -- Def. by S¹ induction. Step 2. -- g-f' : (s : S¹) → (b : P s) → (g ∘ f) (s , b) == id (s , b) -- g-f' = S¹-ind (λ s → (b : P s) → (g ∘ f) (s , b) == id (s , b)) c cpath
Finally, the equivalence:
-- Equiv. -- ΣS¹P-≃-pS : Σ S¹ P ≃ pS -- ΣS¹P-≃-pS = qinv-≃ f (g , f-g , g-f)
- Univalent Foundations Program, T. (2013). Homotopy Type Theory: Univalent Foundations of Mathematics. Institute for Advanced Study. Retrieved from http://saunders.phil.cmu.edu/book/hott-online.pdf