Pathovers
Pathovers
This is a work in progress jointly with Marc Bezem. Some of the following proofs are collapsed or hidden to reduce the size of the document. Nevertheless, the reader can click on them to open the full description. Pictures are also clickable.
Introduction
The type of pathovers can be defined in at least five different ways, all equivalent as we show later in this document (see also (Licata & Brunerie, 2015)).
Let A : Type, a₁, a₂ : A, C : A → Type, c₁ : C a₁ and c₂ : C a₂.
Using the same notation from (Univalent Foundations Program, 2013), one of the definitions for the
Pathover type is as the shorthand for the path between the transport along a
path α : a₁ = a₂ of the point c₁ : C a₁ and the point c₂ in the fiber C
a₂. That is, a pathover is a term that inhabits the type (transport C α c₁) = c₂
also denoted by PathOver C α c₁ c₂.
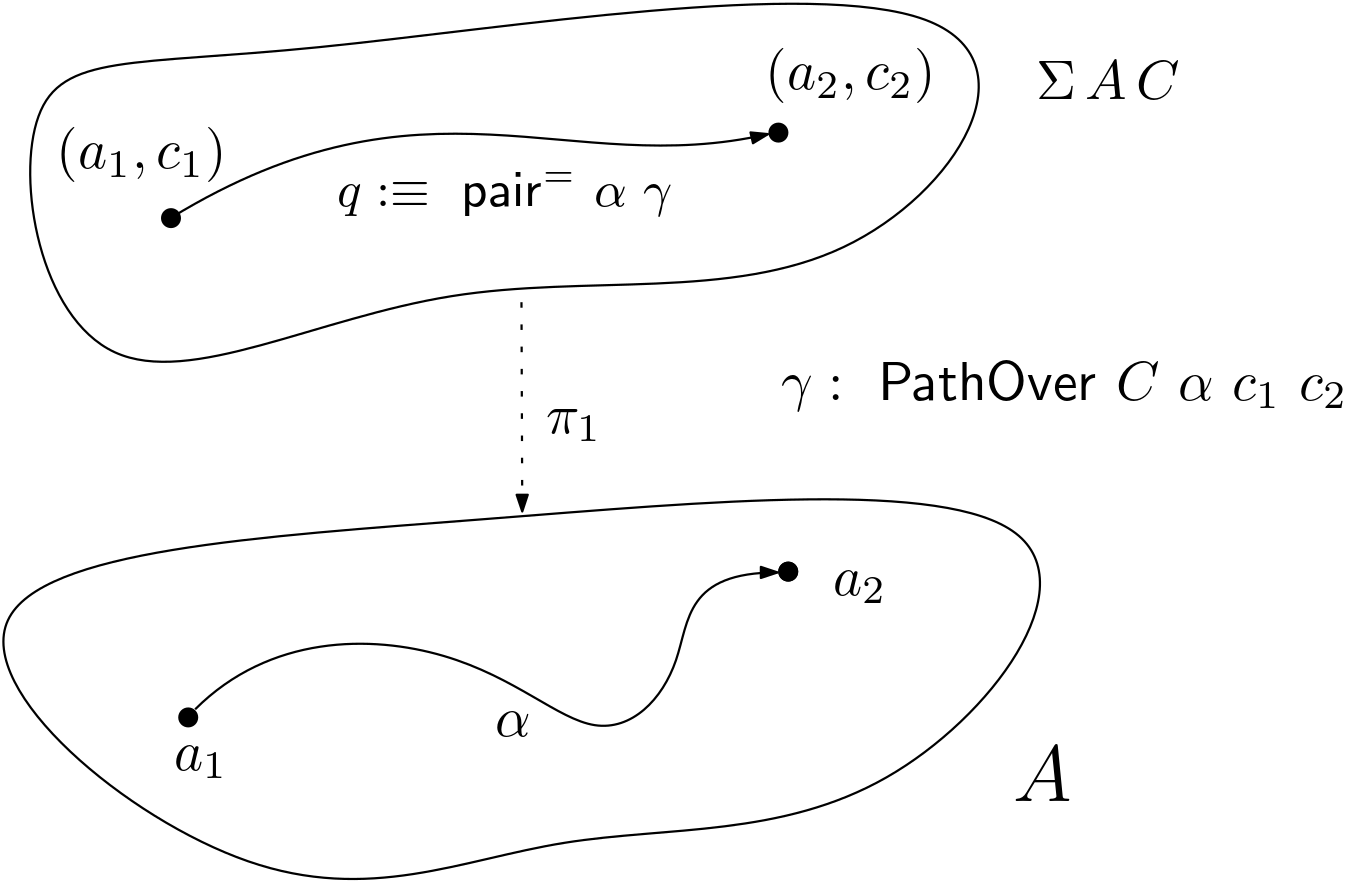 Figure 1. PathOvers and paths in the total space.
Figure 1. PathOvers and paths in the total space.
The term pathover was formally defined in (Licata & Brunerie, 2015) and also
briefly mentioned in Section 2.3 in (Univalent Foundations Program, 2013) as a path in the total
space of C which “lies over” α.
We are interested to prove the geometrical intuition behind these pathovers in
which the path q : (a₁, c₁) = (a₂, c₂) is projected down onto α : a₁ = a₂ as
it follows from the figure showed above. Σ A C is the total space and
“projecting down” means ap π₁ q = α where π₁ : Σ A C → A.
We formalize such a correspondence by showing the following equivalence,
We give two proofs of this equivalence. The second proof uses some results about Σ-types that make the second proof of the equivalence a little shorter. We also believe they can be useful in other contexts.
The correctness of this development has been type-checked by Agda v2.5.4. To be
consistent with homotopy type theory, we tell Agda to not use Axiom K for
type-checking by using the option without-K. Without Axiom K, Agda’s Set is
not a good name for universes in HoTT and we rename Set to Type.
{-# OPTIONS --without-K #-} open import Agda.Primitive using ( Level ; lsuc; _⊔_ ) Type : (ℓ : Level) → Set (lsuc ℓ) Type ℓ = Set ℓ
Now, let us define in Agda the homogeneous equality type and the heterogeneous
equality in order to define in different ways the PathOver type.
Homogeneous equality
The homogeneous equality is the Identity type denoted by Path that relates
two elements a₀ and a₁ whose types are definitionally/judgmentally equal.
We also refer to this type as a₁ == a₂ or Path a₁ a₂.
infix 30 _==_ data _==_ {ℓᵢ} {A : Type ℓᵢ} (a : A) : A → Type ℓᵢ where idp : a == a Path = _==_
Heterogeneous equality
The heterogeneous equality as it is defined in (Licata & Brunerie, 2015) is a type
for equality between two elements a : A, b : B, along an equality α : A == B.
Its terms are constructed by the reflexivity constructor which applies only when
both the two types and the two terms are judgementally equal.
We define in Agda the heterogeneous equality as HEq with a different subindex
for each definition. We start with the inductive definition HEq₁ in the
following.
data HEq₁ {ℓ} (A : Type ℓ) : (B : Type ℓ) → (α : A == B) (a : A) (b : B) → Type (lsuc ℓ) where idp : ∀ {a : A} → HEq₁ A A idp a a
In this definition, the reflexivity constructor for Paths is the same name as the constructor for homogeneous equality. Using the same name will allow us to switch between different definitions of heterogeneous equality in the posteriori proofs and also to switch between the definitions of the Pathover type.
Now, we have two types HEq₂ and HEq₃ that use the transport and the coercion
functions, defined below. To define transport we do path-induction on the
homogeneous equality between the terms and to define coercion (coe) we use
transport. It is also possible to define them in the other way around, that
is, transport by using coe.
transport : ∀ {ℓᵢ ℓⱼ} {A : Type ℓᵢ} (C : A → Type ℓⱼ) {a b : A} → a == b → C a → C b transport C idp = (λ x → x)
coe : ∀ {ℓ}{A B : Type ℓ} → A == B → (A → B) coe p A = transport (λ X → X) p A
--- Basic HoTT types, functions and theorems. module hott where infixr 60 _,_ record Σ {ℓᵢ ℓⱼ} (A : Type ℓᵢ)(C : A → Type ℓⱼ) : Type (ℓᵢ ⊔ ℓⱼ) where constructor _,_ field π₁ : A π₂ : C π₁ open Σ public Π : ∀ {ℓᵢ ℓⱼ} (A : Type ℓᵢ) (P : A → Type ℓⱼ) → Type (ℓᵢ ⊔ ℓⱼ) Π A P = (x : A) → P x _×_ : ∀{ℓᵢ ℓⱼ} (S : Type ℓᵢ) (T : Type ℓⱼ) → Type (ℓᵢ ⊔ ℓⱼ) A × B = Σ A (λ _ → B) infixr 80 _+_ data _+_ {ℓᵢ ℓⱼ} (S : Type ℓᵢ) (T : Type ℓⱼ) : Type (ℓᵢ ⊔ ℓⱼ) where inl : S → S + T inr : T → S + T id : ∀ {ℓ} {A : Type ℓ} → A → A id a = a infixr 80 _∘_ _∘_ : ∀{ℓᵢ ℓⱼ ℓₖ} {A : Type ℓᵢ} {B : A → Type ℓⱼ} {C : (a : A) → (B a → Type ℓₖ)} → (g : {a : A} → Π (B a) (C a)) → (f : Π A B) → Π A (λ a → C a (f a)) g ∘ f = λ x → g (f x) infixr 0 _$_ _$_ : ∀ {i j} {A : Type i} {B : A → Type j} → (∀ x → B x) → (∀ x → B x) f $ x = f x infixl 50 _·_ _·_ : ∀ {ℓ} {A : Type ℓ} {a b c : A} → a == b → b == c → a == c idp · q = q inv : ∀{ℓ} {A : Type ℓ} {a b : A} → a == b → b == a inv idp = idp _⁻¹ = inv ap : ∀{ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} {a b : A} → (f : A → B) → a == b → f a == f b ap f idp = idp module EquationalReasoning {ℓᵢ} {A : Type ℓᵢ} where infixr 2 _==⟨⟩_ _==⟨⟩_ : ∀ (x {y} : A) → x == y → x == y _ ==⟨⟩ p = p infixr 2 _==⟨_⟩_ _==⟨_⟩_ : (x : A) {y z : A} → x == y → y == z → x == z _ ==⟨ p1 ⟩ p2 = p1 · p2 infix 3 _∎ _∎ : (x : A) → x == x _∎ = λ x → idp infix 1 begin_ begin_ : {x y : A} → x == y → x == y begin_ p = p open EquationalReasoning public module ·-Properties {ℓ} {A : Type ℓ} where involution : {a b : A} {p : a == b} → inv (inv p) == p involution {p = idp} = idp ·-runit : {a b : A} (p : a == b) → p == p · idp ·-runit idp = idp ·-runit-infer : {a b : A} {p : a == b} → p · idp == p ·-runit-infer {p = idp} = idp ·-lunit : {a b : A} (p : a == b) → p == idp · p ·-lunit idp = idp ·-assoc : {a b c d : A} (p : a == b) → (q : b == c) → (r : c == d) → (p · q) · r == p · (q · r) ·-assoc idp q r = idp ·-linv : {a b : A} (p : a == b) → (inv p) · p == idp ·-linv idp = idp ·-rinv : {a b : A} (p : a == b) → p · (inv p) == idp ·-rinv idp = idp ·-cancellation : {a : A} (p : a == a) → (q : a == a) → p · q == p → q == idp ·-cancellation {a} p q α = begin q ==⟨ ap (_· q) (inv (·-linv p)) ⟩ inv p · p · q ==⟨ (·-assoc (inv p) _ _) ⟩ inv p · (p · q) ==⟨ (ap (inv p ·_) α) ⟩ inv p · p ==⟨ ·-linv p ⟩ idp ∎ open ·-Properties public module Transport-Properties {ℓᵢ} {A : Type ℓᵢ} where -- Some lemmas on the transport operation. transport-const : ∀ {ℓⱼ} {P : A → Type ℓⱼ} {x y : A} {B : Type ℓᵢ} → (p : x == y) → (b : B) → transport (λ _ → B) p b == b transport-const idp _ = idp transport-concat-r : {a : A} {x y : A} → (p : x == y) → (q : a == x) → transport (λ x → a == x) p q == q · p transport-concat-r idp q = ·-runit q transport-concat-l : {a : A} {x y : A} → (p : x == y) → (q : x == a) → transport (λ x → x == a) p q == (inv p) · q transport-concat-l idp q = idp transport-concat : {x y : A} → (p : x == y) → (q : x == x) → transport (λ x → x == x) p q == (inv p) · q · p transport-concat idp q = ·-runit q transport-eq-fun : ∀{ℓⱼ} {B : Type ℓⱼ} (f g : A → B) {x y : A} (p : x == y) (q : f x == g x) → transport (λ z → f z == g z) p q == inv (ap f p) · q · (ap g p) transport-eq-fun f g idp q = ·-runit q transport-comp : ∀{ℓⱼ} {a b c : A} {P : A → Type ℓⱼ} (p : a == b) (q : b == c) → ((transport P q) ∘ (transport P p)) == transport P (p · q) transport-comp {P = P} idp q = idp {a = (transport P q)} transport-comp-h : ∀{ℓⱼ} {a b c : A} {P : A → Type ℓⱼ} (p : a == b) (q : b == c) (x : P a) → ((transport P q) ∘ (transport P p)) x == transport P (p · q) x transport-comp-h {P = P} idp q x = idp {a = (transport P q x)} -- A shorter notation for transport. _✶ : ∀ {ℓⱼ} {P : A → Type ℓⱼ} {a b : A} → a == b → P a → P b _✶ {ℓⱼ} {P} = transport {ℓᵢ = ℓᵢ} {ℓⱼ = ℓⱼ} P open Transport-Properties public ap-id : ∀{ℓᵢ} {A : Type ℓᵢ} {a b : A} (p : a == b) → ap id p == p ap-id idp = idp ap-comp : ∀{ℓᵢ ℓⱼ ℓₖ} {A : Type ℓᵢ} {B : Type ℓⱼ} {C : Type ℓₖ} {a b : A} → (f : A → B) → (g : B → C) → (p : a == b) → ap g (ap f p) == ap (g ∘ f) p ap-comp f g idp = idp ap-const : ∀{ℓᵢ ℓⱼ} {A : Type ℓᵢ} {C : Type ℓⱼ} {a b : A} {c : C} (p : a == b) → ap (λ _ → c) p == idp ap-const {c = c} idp = idp {a = idp {a = c}} ap-· : ∀{ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} {a b c : A} → (f : A → B) → (p : a == b) → (q : b == c) → ap f (p · q) == ap f p · ap f q ap-· f idp q = idp {a = (ap f q)} ap-inv : ∀{ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} {a b : A} → (f : A → B) → (p : a == b) → ap f (inv p) == inv (ap f p) ap-inv f idp = idp transport-eq-fun-l : ∀{ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} {b : B} (f : A → B) {x y : A} → (p : x == y) (q : f x == b) → transport (λ z → f z == b) p q == inv (ap f p) · q transport-eq-fun-l {b = b} f p q = begin transport (λ z → f z == b) p q ==⟨ transport-eq-fun f (λ _ → b) p q ⟩ inv (ap f p) · q · ap (λ _ → b) p ==⟨ ap (inv (ap f p) · q ·_) (ap-const p) ⟩ inv (ap f p) · q · idp ==⟨ inv (·-runit _) ⟩ inv (ap f p) · q ∎ transport-eq-fun-r : ∀{ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} {b : B} (g : A → B) {x y : A} → (p : x == y) (q : b == g x) → transport (λ z → b == g z) p q == q · (ap g p) transport-eq-fun-r {b = b} g p q = begin transport (λ z → b == g z) p q ==⟨ transport-eq-fun (λ _ → b) g p q ⟩ inv (ap (λ _ → b) p) · q · ap g p ==⟨ ·-assoc (inv (ap (λ _ → b) p)) q (ap g p) ⟩ inv (ap (λ _ → b) p) · (q · ap g p) ==⟨ ap (λ u → inv u · (q · ap g p)) (ap-const p) ⟩ (q · ap g p) ∎ transport-inv-l : ∀{ℓ} {A B : Type ℓ} → (p : A == B) → (b : B) → transport (λ v → v) p (transport (λ v → v) (inv p) b) == b transport-inv-l idp b = idp transport-inv-r : ∀{ℓ} {A B : Type ℓ} → (p : A == B) → (a : A) → transport (λ v → v) (inv p) (transport (λ v → v) p a) == a transport-inv-r idp b = idp transport-family : ∀{ℓᵢ ℓⱼ ℓₖ} {A : Type ℓᵢ} {B : Type ℓⱼ} {P : B → Type ℓₖ} → {f : A → B} → {x y : A} → (p : x == y) → (u : P (f x)) → transport (P ∘ f) p u == transport P (ap f p) u transport-family idp u = idp transport-family-id : ∀{ℓᵢ ℓₖ} {A : Type ℓᵢ} {P : A → Type ℓₖ} → {x y : A} → (p : x == y) → (u : P x) → transport (λ a → P a) p u == transport P p u transport-family-id idp u = idp transport-fun : ∀{ℓᵢ ℓⱼ ℓₖ} {X : Type ℓᵢ} {x y : X} {A : X → Type ℓⱼ} {B : X → Type ℓₖ} → (p : x == y) → (f : A x → B x) → transport (λ x → (A x → B x)) p f == (λ x → transport B p (f (transport A (inv p) x))) transport-fun idp f = idp apd : ∀{ℓᵢ ℓⱼ} {A : Type ℓᵢ} {P : A → Type ℓⱼ} {a b : A} → (f : (a : A) → P a) → (p : a == b) → transport P p (f a) == f b apd f idp = idp module Homotopy {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {P : A → Type ℓⱼ} where -- A homotopy is a natural isomorphism between two functions, we will write -- f ∼ g when (f x == g x) for all x. homotopy : (f g : ((x : A) → P x)) → Type (ℓᵢ ⊔ ℓⱼ) homotopy f g = (x : A) → f x == g x _∼_ : (f g : ((x : A) → P x)) → Type (ℓᵢ ⊔ ℓⱼ) f ∼ g = homotopy f g -- Homotopy is an equivalence relation h-refl : (f : (x : A) → P x) → f ∼ f h-refl f x = idp h-simm : (f g : (x : A) → P x) → f ∼ g → g ∼ f h-simm f g u x = inv (u x) h-comp : (f g h : (x : A) → P x) → f ∼ g → g ∼ h → f ∼ h h-comp f g h u v x = (u x)·(v x) _●_ : {f g h : (x : A) → P x} → f ∼ g → g ∼ h → f ∼ h α ● β = h-comp _ _ _ α β open Homotopy public -- Composition with homotopies module HomotopyComposition {ℓᵢ ℓⱼ ℓₖ} {A : Type ℓᵢ} {B : Type ℓⱼ} {C : Type ℓₖ} where hl-comp : (f g : A → B) → (j k : B → C) → f ∼ g → j ∼ k → (j ∘ f) ∼ (k ∘ g) hl-comp f g j k α β x = ap j (α x) · β (g x) rcomp-∼ : (f : A → B) → {j k : B → C} → j ∼ k → (j ∘ f) ∼ (k ∘ f) rcomp-∼ f β = hl-comp _ _ _ _ (h-refl f) β lcomp-∼ : {f g : A → B} → (j : B → C) → f ∼ g → (j ∘ f) ∼ (j ∘ g) lcomp-∼ j α = hl-comp _ _ _ _ α (h-refl j) open HomotopyComposition public module Fibers {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} where -- The fiber of a map over a point is given by fib : (f : A → B) → B → Type (ℓᵢ ⊔ ℓⱼ) fib f b = Σ A (λ a → f a == b) -- A function applied over the fiber returns the original point fib-eq : {f : A → B} → {b : B} → (h : fib f b) → f (π₁ h) == b fib-eq (a , α) = α -- Each point is on the fiber of its image fib-image : {f : A → B} → {a : A} → fib f (f a) fib-image {f} {a} = a , idp open Fibers public module Contractible where -- Contractible types. A contractible type is a type such that every -- element is equal to a center of contraction. isContr : ∀{ℓ} (A : Type ℓ) → Type ℓ isContr A = Σ A (λ a → ((x : A) → a == x)) open Contractible public module Equivalence where module DefinitionOfEquivalence {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} where -- Contractible maps. A map is contractible if the fiber in any -- point is contractible, that is, each element has a unique -- preimage. isContrMap : (f : A → B) → Type (ℓᵢ ⊔ ℓⱼ) isContrMap f = (b : B) → isContr (fib f b) -- There exists an equivalence between two types if there exists a -- contractible function between them. isEquiv : (f : A → B) → Type (ℓᵢ ⊔ ℓⱼ) isEquiv = isContrMap open DefinitionOfEquivalence public -- Equivalence of types. _≃_ : ∀{ℓᵢ ℓⱼ} (A : Type ℓᵢ) (B : Type ℓⱼ) → Type (ℓᵢ ⊔ ℓⱼ) A ≃ B = Σ (A → B) isEquiv module EquivalenceMaps {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} where -- Maps of an equivalence lemap : A ≃ B → (A → B) lemap = π₁ fun≃ = lemap remap : A ≃ B → (B → A) remap (f , contrf) b = π₁ (π₁ (contrf b)) -- The maps of an equivalence are inverses in particular lrmap-inverse : (eq : A ≃ B) → {b : B} → (lemap eq) ((remap eq) b) == b lrmap-inverse (f , eqf) {b} = fib-eq (π₁ (eqf b)) rlmap-inverse : (eq : A ≃ B) → {a : A} → (remap eq) ((lemap eq) a) == a rlmap-inverse (f , eqf) {a} = ap π₁ ((π₂ (eqf (f a))) fib-image) lrmap-inverse-h : (eq : A ≃ B) → ((lemap eq) ∘ (remap eq)) ∼ id lrmap-inverse-h eq = λ x → lrmap-inverse eq {x} rlmap-inverse-h : (eq : A ≃ B) → ((remap eq) ∘ (lemap eq)) ∼ id rlmap-inverse-h eq = λ x → rlmap-inverse eq {x} open EquivalenceMaps public open Equivalence public module FunctionExtensionality {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : A → Type ℓⱼ} {f g : (a : A) → B a} where -- Application of an homotopy happly : f == g → ((x : A) → f x == g x) happly idp x = idp -- The axiom of function extensionality postulates that the -- application of homotopies is an equivalence. postulate axiomFunExt : isEquiv happly eqFunExt : (f == g) ≃ ((x : A) → f x == g x) eqFunExt = happly , axiomFunExt -- From this, the usual notion of function extensionality follows. funext : ((x : A) → f x == g x) → f == g funext = remap eqFunExt -- Beta and eta rules for function extensionality funext-β : (h : ((x : A) → f x == g x)) → happly (funext h) == h funext-β h = lrmap-inverse eqFunExt funext-η : (p : f == g) → funext (happly p) == p funext-η p = rlmap-inverse eqFunExt open FunctionExtensionality public -- Function extensionality in the transport case module FunctionExtensionalityTransport {ℓᵢ ℓⱼ} {X : Type ℓᵢ} {A B : X → Type ℓⱼ} {x y : X} where funext-transport : (p : x == y) → (f : A x → B x) → (g : A y → B y) → ((p ✶) f == g) ≃ ((a : A(x)) → (p ✶) (f a) == g ((p ✶) a)) funext-transport idp f g = eqFunExt funext-transport-l : (p : x == y) → (f : A x → B x) → (g : A y → B y) → ((p ✶) f == g) → ((a : A(x)) → (p ✶) (f a) == g ((p ✶) a)) funext-transport-l p f g = lemap (funext-transport p _ _) funext-transport-r : (p : x == y) → (f : A x → B x) → (g : A y → B y) → ((a : A(x)) → (p ✶) (f a) == g ((p ✶) a)) → ((p ✶) f == g) funext-transport-r p f g = remap (funext-transport p _ _) open FunctionExtensionalityTransport public module Sigma {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {P : A → Type ℓⱼ} where -- Two dependent pairs are equal if they are componentwise equal. Σ-componentwise : {v w : Σ A P} → v == w → Σ (π₁ v == π₁ w) (λ p → (p ✶) (π₂ v) == π₂ w) Σ-componentwise idp = (idp , idp) Σ-bycomponents : {v w : Σ A P} → Σ (π₁ v == π₁ w) (λ p → (p ✶) (π₂ v) == π₂ w) → v == w Σ-bycomponents (idp , idp) = idp pair= = Σ-bycomponents uppt : (x : Σ A P) → (π₁ x , π₂ x) == x uppt (a , b) = idp Σ-ap-π₁ : {a₁ a₂ : A} {b₁ : P a₁} {b₂ : P a₂} → (α : a₁ == a₂) → (γ : transport P α b₁ == b₂) → ap π₁ (pair= (α , γ)) == α Σ-ap-π₁ idp idp = idp ap-π₁-pair= = Σ-ap-π₁ open Sigma public module CartesianProduct {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} where -- In a pair, the equality of the two components of the pairs is -- equivalent to equality of the two pairs. prodComponentwise : {x y : A × B} → (x == y) → ((π₁ x == π₁ y) × (π₂ x == π₂ y)) π₁ (prodComponentwise idp) = idp π₂ (prodComponentwise idp) = idp prodByComponents : {x y : A × B} → ((π₁ x == π₁ y) × (π₂ x == π₂ y)) → (x == y) prodByComponents (idp , idp) = idp -- This is in fact an equivalence. prodCompInverse : {x y : A × B} (b : ((π₁ x == π₁ y) × (π₂ x == π₂ y))) → prodComponentwise (prodByComponents b) == b prodCompInverse (idp , idp) = idp prodByCompInverse : {x y : A × B} (b : x == y) → prodByComponents (prodComponentwise b) == b prodByCompInverse idp = idp open CartesianProduct public module Propositions where -- A type is a mere proposition if any two inhabitants of the type -- are equal isProp : ∀{ℓ} (A : Type ℓ) → Type ℓ isProp A = ((x y : A) → x == y) -- The type of mere propositions hProp : ∀{ℓ} → Type (lsuc ℓ) hProp {ℓ} = Σ (Type ℓ) isProp -- The dependent function type to proposition types is itself a -- proposition. piProp : ∀{ℓᵢ ℓⱼ} → {A : Type ℓᵢ} → {B : A → Type ℓⱼ} → ((a : A) → isProp (B a)) → isProp ((a : A) → B a) piProp props f g = funext λ a → props a (f a) (g a) -- The product of propositions is itself a proposition. isProp-prod : ∀{ℓᵢ ℓⱼ} → {A : Type ℓᵢ} → {B : Type ℓⱼ} → isProp A → isProp B → isProp (A × B) isProp-prod p q x y = prodByComponents ((p _ _) , (q _ _)) open Propositions public module Sets where -- A type is a "set" by definition if any two equalities on the type -- are equal. isSet : ∀{ℓ} (A : Type ℓ) → Type ℓ isSet A = (x y : A) → isProp (x == y) -- The type of sets. hSet : ∀{ℓ} → Type (lsuc ℓ) hSet {ℓ} = Σ (Type ℓ) isSet -- Product of sets is a set. isSet-prod : ∀{ℓᵢ ℓⱼ} {A : Type ℓᵢ} → {B : Type ℓⱼ} → isSet A → isSet B → isSet (A × B) isSet-prod sa sb (a , b) (c , d) p q = begin p ==⟨ inv (prodByCompInverse p) ⟩ prodByComponents (prodComponentwise p) ==⟨ ap prodByComponents (prodByComponents (sa a c _ _ , sb b d _ _)) ⟩ prodByComponents (prodComponentwise q) ==⟨ prodByCompInverse q ⟩ q ∎ open Sets public module HLevels where -- Propositions are Sets. propIsSet : ∀{ℓ} {A : Type ℓ} → isProp A → isSet A propIsSet {A = A} f a _ p q = lemma p · inv (lemma q) where triang : {y z : A} {p : y == z} → (f a y) · p == f a z triang {b}{p = idp} = inv (·-runit (f a b)) lemma : {y z : A} (p : y == z) → p == inv (f a y) · (f a z) lemma {y} {z} p = begin p ==⟨ ap (_· p) (inv (·-linv (f a y))) ⟩ inv (f a y) · f a y · p ==⟨ ·-assoc (inv (f a y)) (f a y) p ⟩ inv (f a y) · (f a y · p) ==⟨ ap (inv (f a y) ·_) triang ⟩ inv (f a y) · (f a z) ∎ -- Contractible types are Propositions. contrIsProp : ∀{ℓ} {A : Type ℓ} → isContr A → isProp A contrIsProp (a , p) x y = inv (p x) · p y -- To be contractible is itself a proposition. isContrIsProp : ∀{ℓ} {A : Type ℓ} → isProp (isContr A) isContrIsProp {_} {A} (a , p) (b , q) = Σ-bycomponents (inv (q a) , piProp (AisSet b) _ q) where AisSet : isSet A AisSet = propIsSet (contrIsProp (a , p)) open HLevels public module EquivalenceProp {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} where -- Contractible maps are propositions isContrMapIsProp : (f : A → B) → isProp (isContrMap f) isContrMapIsProp f = piProp λ a → isContrIsProp isEquivIsProp : (f : A → B) → isProp (isEquiv f) isEquivIsProp = isContrMapIsProp -- Equality of same-morphism equivalences sameEqv : {α β : A ≃ B} → π₁ α == π₁ β → α == β sameEqv {(f , σ)} {(g , τ)} p = Σ-bycomponents (p , (isEquivIsProp g _ τ)) -- Equivalences preserve propositions isProp-≃ : (A ≃ B) → isProp A → isProp B isProp-≃ eq prop x y = begin x ==⟨ inv (lrmap-inverse eq) ⟩ lemap eq ((remap eq) x) ==⟨ ap (λ u → lemap eq u) (prop _ _) ⟩ lemap eq ((remap eq) y) ==⟨ lrmap-inverse eq ⟩ y ∎ open EquivalenceProp public module Naturality {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} where h-naturality : {f g : A → B} (H : f ∼ g) → {x y : A} → (p : x == y) → H x · ap g p == ap f p · H y h-naturality H {x = x} (idp ) = inv (·-runit (H x)) open Naturality h-naturality-id : ∀{ℓ} {A : Type ℓ} {f : A → A} (H : f ∼ id) → {x : A} → H (f x) == ap f (H x) h-naturality-id {f = f} H {x = x} = begin H (f x) ==⟨ ·-runit (H (f x)) ⟩ H (f x) · (idp {a = f x}) ==⟨ ap (H (f x) ·_) (inv (·-rinv (H x))) ⟩ H (f x) · (H x · inv (H x)) ==⟨ inv (·-assoc (H (f x)) _ (inv (H x))) ⟩ H (f x) · H x · inv (H x) ==⟨ ap (λ u → H (f x) · u · inv (H x)) (inv (ap-id _)) ⟩ H (f x) · ap id (H x) · inv (H x) ==⟨ ap (_· inv (H x)) (h-naturality H (H x)) ⟩ ap f (H x) · H x · inv (H x) ==⟨ ·-assoc (ap f (H x)) _ (inv (H x)) ⟩ ap f (H x) · (H x · inv (H x)) ==⟨ ap (ap f (H x) ·_) (·-rinv (H x)) ⟩ ap f (H x) · (idp {a = f x}) ==⟨ inv (·-runit (ap f (H x))) ⟩ ap f (H x) ∎ module Halfadjoints {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} where -- Half adjoint equivalence. record ishae (f : A → B) : Type (ℓᵢ ⊔ ℓⱼ) where constructor hae field g : B → A η : (g ∘ f) ∼ id ε : (f ∘ g) ∼ id τ : (a : A) → ap f (η a) == ε (f a) -- Half adjoint equivalences give contractible fibers. ishae-contr : (f : A → B) → ishae f → isContrMap f ishae-contr f (hae g η ε τ) y = ((g y) , (ε y)) , contra where lemma : (c c' : fib f y) → Σ (π₁ c == π₁ c') (λ γ → (ap f γ) · π₂ c' == π₂ c) → c == c' lemma c c' (p , q) = Σ-bycomponents (p , lemma2) where lemma2 : transport (λ z → f z == y) p (π₂ c) == π₂ c' lemma2 = begin transport (λ z → f z == y) p (π₂ c) ==⟨ transport-eq-fun-l f p (π₂ c) ⟩ inv (ap f p) · (π₂ c) ==⟨ ap (inv (ap f p) ·_) (inv q) ⟩ inv (ap f p) · ((ap f p) · (π₂ c')) ==⟨ inv (·-assoc (inv (ap f p)) (ap f p) (π₂ c')) ⟩ inv (ap f p) · (ap f p) · (π₂ c') ==⟨ ap (_· (π₂ c')) (·-linv (ap f p)) ⟩ π₂ c' ∎ contra : (x : fib f y) → (g y , ε y) == x contra (x , p) = lemma (g y , ε y) (x , p) (γ , lemma3) where γ : g y == x γ = inv (ap g p) · η x lemma3 : (ap f γ · p) == ε y lemma3 = begin ap f γ · p ==⟨ ap (_· p) (ap-· f (inv (ap g p)) (η x)) ⟩ ap f (inv (ap g p)) · ap f (η x) · p ==⟨ ·-assoc (ap f (inv (ap g p))) _ p ⟩ ap f (inv (ap g p)) · (ap f (η x) · p) ==⟨ ap (_· (ap f (η x) · p)) (ap-inv f (ap g p)) ⟩ inv (ap f (ap g p)) · (ap f (η x) · p) ==⟨ ap (λ u → inv (ap f (ap g p)) · (u · p)) (τ x) ⟩ inv (ap f (ap g p)) · (ε (f x) · p) ==⟨ ap (λ u → inv (ap f (ap g p)) · (ε (f x) · u)) (inv (ap-id p)) ⟩ inv (ap f (ap g p)) · (ε (f x) · ap id p) ==⟨ ap (inv (ap f (ap g p)) ·_) (h-naturality ε p) ⟩ inv (ap f (ap g p)) · (ap (f ∘ g) p · ε y) ==⟨ ap (λ u → inv u · (ap (f ∘ g) p · ε y)) (ap-comp g f p) ⟩ inv (ap (f ∘ g) p) · (ap (f ∘ g) p · ε y) ==⟨ inv (·-assoc (inv (ap (f ∘ g) p)) _ (ε y)) ⟩ (inv (ap (f ∘ g) p) · ap (f ∘ g) p) · ε y ==⟨ ap (_· ε y) (·-linv (ap (λ z → f (g z)) p)) ⟩ ε y ∎ -- Half-adjointness implies equivalence. ishae-≃ : {f : A → B} → ishae f → A ≃ B ishae-≃ ishaef = _ , (ishae-contr _ ishaef) open Halfadjoints public module Quasiinverses {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} where -- Definitions for quasi-inverses, left-inverses, right-inverses and -- biinverses. qinv : (A → B) → Type (ℓᵢ ⊔ ℓⱼ) qinv f = Σ (B → A) (λ g → ((f ∘ g) ∼ id) × ((g ∘ f) ∼ id)) linv : (A → B) → Type (ℓᵢ ⊔ ℓⱼ) linv f = Σ (B → A) (λ g → (g ∘ f) ∼ id) rinv : (A → B) → Type (ℓᵢ ⊔ ℓⱼ) rinv f = Σ (B → A) λ g → (f ∘ g) ∼ id biinv : (A → B) → Type (ℓᵢ ⊔ ℓⱼ) biinv f = linv f × rinv f qinv-biinv : (f : A → B) → qinv f → biinv f qinv-biinv f (g , (u1 , u2)) = (g , u2) , (g , u1) biinv-qinv : (f : A → B) → biinv f → qinv f biinv-qinv f ((h , α) , (g , β)) = g , (β , δ) where γ1 : g ∼ ((h ∘ f) ∘ g) γ1 = rcomp-∼ g (h-simm (h ∘ f) id α) γ2 : ((h ∘ f) ∘ g) ∼ (h ∘ (f ∘ g)) γ2 x = idp γ : g ∼ h γ = γ1 ● (γ2 ● (lcomp-∼ h β)) δ : (g ∘ f) ∼ id δ = (rcomp-∼ f γ) ● α equiv-biinv : (f : A → B) → isContrMap f → biinv f equiv-biinv f contrf = (remap eq , rlmap-inverse-h eq) , (remap eq , lrmap-inverse-h eq) where eq : A ≃ B eq = f , contrf -- Quasiinverses are halfadjoint equivalences. qinv-ishae : {f : A → B} → qinv f → ishae f qinv-ishae {f} (g , (ε , η)) = record { g = g ; η = η ; ε = λ b → inv (ε (f (g b))) · ap f (η (g b)) · ε b ; τ = τ } where lemma1 : (a : A) → ap f (η (g (f a))) · ε (f a) == ε (f (g (f a))) · ap f (η a) lemma1 a = begin ap f (η ((g ∘ f) a)) · ε (f a) ==⟨ ap (λ u → ap f u · ε (f a)) (h-naturality-id η) ⟩ ap f (ap (g ∘ f) (η a)) · ε (f a) ==⟨ ap (_· ε (f a)) (ap-comp (g ∘ f) f (η a)) ⟩ ap (f ∘ (g ∘ f)) (η a) · ε (f a) ==⟨ inv (h-naturality (λ x → ε (f x)) (η a)) ⟩ ε (f (g (f a))) · ap f (η a) ∎ τ : (a : A) → ap f (η a) == (inv (ε (f (g (f a)))) · ap f (η (g (f a))) · ε (f a)) τ a = begin ap f (η a) ==⟨ ap (_· ap f (η a)) (inv (·-linv (ε (f (g (f a)))))) ⟩ inv (ε (f (g (f a)))) · ε (f (g (f a))) · ap f (η a) ==⟨ ·-assoc (inv (ε (f (g (f a))))) _ (ap f (η a)) ⟩ inv (ε (f (g (f a)))) · (ε (f (g (f a))) · ap f (η a)) ==⟨ ap (inv (ε (f (g (f a)))) ·_) (inv (lemma1 a)) ⟩ inv (ε (f (g (f a)))) · (ap f (η (g (f a))) · ε (f a)) ==⟨ inv (·-assoc (inv (ε (f (g (f a))))) _ (ε (f a))) ⟩ inv (ε (f (g (f a)))) · ap f (η (g (f a))) · ε (f a) ∎ -- Quasiinverses create equivalences. qinv-≃ : (f : A → B) → qinv f → A ≃ B qinv-≃ f = ishae-≃ ∘ qinv-ishae ≃-qinv : A ≃ B → Σ (A → B) qinv ≃-qinv eq = lemap eq , (remap eq , (lrmap-inverse-h eq , rlmap-inverse-h eq)) -- Half-adjoint equivalences are quasiinverses. ishae-qinv : {f : A → B} → ishae f → qinv f ishae-qinv {f} (hae g η ε τ) = g , (ε , η) ≃-ishae : (e : A ≃ B)→ ishae (lemap e) ≃-ishae e = qinv-ishae (π₂ (≃-qinv e)) open Quasiinverses public module EquivalenceComposition where -- Composition of quasiinverses qinv-comp : ∀{ℓ} {A B C : Type ℓ} → Σ (A → B) qinv → Σ (B → C) qinv → Σ (A → C) qinv qinv-comp (f , (if , (εf , ηf))) (g , (ig , (εg , ηg))) = (g ∘ f) , ((if ∘ ig) , ( (λ x → ap g (εf (ig x)) · εg x) , λ x → ap if (ηg (f x)) · ηf x)) qinv-inv : ∀{ℓ} {A B : Type ℓ} → Σ (A → B) qinv → Σ (B → A) qinv qinv-inv (f , (g , (ε , η))) = g , (f , (η , ε)) -- Composition of equivalences idEqv : ∀{ℓ} {A : Type ℓ} → A ≃ A idEqv = id , λ a → (a , idp) , λ { (_ , idp) → idp } compEqv : ∀{ℓ} {A B C : Type ℓ} → A ≃ B → B ≃ C → A ≃ C compEqv {ℓ} {A} {B} {C} eqf eqg = qinv-≃ (π₁ qcomp) (π₂ qcomp) where qcomp : Σ (A → C) qinv qcomp = qinv-comp (≃-qinv eqf) (≃-qinv eqg) invEqv : ∀{ℓ} {A B : Type ℓ} → A ≃ B → B ≃ A invEqv {ℓ} {A} {B} eqf = qinv-≃ (π₁ qcinv) (π₂ qcinv) where qcinv : Σ (B → A) qinv qcinv = qinv-inv (≃-qinv eqf) -- Lemmas about composition compEqv-inv : ∀{ℓ} {A B : Type ℓ} → (α : A ≃ B) → compEqv α (invEqv α) == idEqv compEqv-inv {_} {A} {B} α = sameEqv ( begin π₁ (compEqv α (invEqv α)) ==⟨ idp ⟩ π₁ (invEqv α) ∘ π₁ α ==⟨ funext (rlmap-inverse-h α) ⟩ id ∎) open EquivalenceComposition public module SigmaEquivalence {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {P : A → Type ℓⱼ} where pair=Equiv : {v w : Σ A P} → Σ (π₁ v == π₁ w) (λ p → (p ✶) (π₂ v) == π₂ w) ≃ v == w pair=Equiv = qinv-≃ Σ-bycomponents (Σ-componentwise , HΣ₁ , HΣ₂) where HΣ₁ : Σ-bycomponents ∘ Σ-componentwise ∼ id HΣ₁ idp = idp HΣ₂ : Σ-componentwise ∘ Σ-bycomponents ∼ id HΣ₂ (idp , idp) = idp private f : {a₁ a₂ : A} {α : a₁ == a₂}{c₁ : P a₁} {c₂ : P a₂} → {β : a₁ == a₂} → {γ : transport P β c₁ == c₂} → ap π₁ (pair= (β , γ)) == α → β == α f {β = idp} {γ = idp} idp = idp g : {a₁ a₂ : A} {α : a₁ == a₂}{c₁ : P a₁} {c₂ : P a₂} → {β : a₁ == a₂} → {γ : transport P β c₁ == c₂} → β == α → ap π₁ (pair= (β , γ)) == α g {β = idp} {γ = idp} idp = idp f-g : {a₁ a₂ : A} {α : a₁ == a₂}{c₁ : P a₁} {c₂ : P a₂} → {β : a₁ == a₂} → {γ : transport P β c₁ == c₂} → f {α = α}{β = β}{γ} ∘ g {α = α}{β = β} ∼ id f-g {β = idp} {γ = idp} idp = idp g-f : {a₁ a₂ : A} {α : a₁ == a₂}{c₁ : P a₁} {c₂ : P a₂} → {β : a₁ == a₂} → {γ : transport P β c₁ == c₂} → g {α = α}{β = β}{γ} ∘ f {α = α}{β = β}{γ} ∼ id g-f {β = idp} {γ = idp} idp = idp ap-π₁-pair=Equiv : {a₁ a₂ : A} {c₁ : P a₁} {c₂ : P a₂} → (α : a₁ == a₂) → (γ : Σ (a₁ == a₂) (λ α' → transport P α' c₁ == c₂)) → (ap π₁ (pair= γ) == α) ≃ π₁ γ == α ap-π₁-pair=Equiv {a₁ = a₁} α (β , γ) = qinv-≃ f (g , f-g , g-f) open SigmaEquivalence public -- Univalence Axiom definition. module Univalence where -- Voevodsky's Univalence Axiom. module UnivalenceAxiom {ℓ} {A B : Type ℓ} where idtoeqv : A == B → A ≃ B idtoeqv p = qinv-≃ (transport (λ x → x) p) (transport (λ x → x) (inv p) , (transport-inv-l p , transport-inv-r p)) -- The Univalence axiom induces an equivalence between equalities -- and equivalences. postulate axiomUnivalence : isEquiv idtoeqv eqvUnivalence : (A == B) ≃ (A ≃ B) eqvUnivalence = idtoeqv , axiomUnivalence -- Introduction rule for equalities. ua : A ≃ B → A == B ua = remap eqvUnivalence -- Computation rules ua-β : (eqv : A ≃ B) → idtoeqv (ua eqv) == eqv ua-β eqv = lrmap-inverse eqvUnivalence ua-η : (p : A == B) → ua (idtoeqv p) == p ua-η p = rlmap-inverse eqvUnivalence open UnivalenceAxiom public open Univalence public module EquivalenceReasoning where infixr 2 _≃⟨⟩_ _≃⟨⟩_ : ∀ {ℓ} (A {B} : Type ℓ) → A ≃ B → A ≃ B _ ≃⟨⟩ e = e infixr 2 _≃⟨_⟩_ _≃⟨_⟩_ : ∀ {ℓ} (A : Type ℓ) {B C : Type ℓ} → A ≃ B → B ≃ C → A ≃ C _ ≃⟨ e₁ ⟩ e₂ = compEqv e₁ e₂ -- infix 3 _≃∎ _≃∎ : ∀ {ℓ} (A : Type ℓ) → A ≃ A _≃∎ = λ A → idEqv {A = A} infix 1 begin≃_ begin≃_ : ∀ {ℓ} {A B : Type ℓ} → A ≃ B → A ≃ B begin≃_ e = e open EquivalenceReasoning public module TransportUA where transport-family-ap : ∀ {ℓ} {A : Type ℓ} → (B : A → Type ℓ) → {x y : A} → (p : x == y) → (u : B x) --------------------------------------------------- → transport B p u == transport (λ X → X) (ap B p) u transport-family-ap B idp u = idp transport-family-idtoeqv : ∀ {ℓ} {A : Type ℓ} → (B : A → Type ℓ) → {x y : A} → (p : x == y) → (u : B x) --------------------------------------------------- → transport B p u == fun≃ (idtoeqv (ap B p)) u transport-family-idtoeqv B idp u = idp transport-ua : ∀ {ℓ} {A : Type ℓ} → (B : A → Type ℓ) → {x y : A} → (p : x == y) → (e : B x ≃ B y) → ap B p == ua e ----------------- → (u : B x) → transport B p u == (fun≃ e) u transport-ua B idp e q u = begin transport B idp u ==⟨ transport-family-idtoeqv B idp u ⟩ fun≃ (idtoeqv (ap B idp)) u ==⟨ ap (λ r → fun≃ (idtoeqv r) u) q ⟩ fun≃ (idtoeqv (ua e)) u ==⟨ ap (λ r → fun≃ r u) (ua-β e) ⟩ fun≃ e u ∎ open TransportUA public open hott public
Let be α : A == B, a : A, and b : B then the following types are equivalent
to the previous type HEq₁.
HEq₂ : ∀ {ℓ} (A : Type ℓ)(B : Type ℓ) (α : A == B)(a : A)(b : B) → Type ℓ HEq₂ A B α a b = Path (coe α a) b
HEq₃ : ∀ {ℓ} (A : Type ℓ)(B : Type ℓ) (α : A == B)(a : A)(b : B) → Type ℓ HEq₃ A B α a b = Path a (coe (inv α) b)
HEq₄ : ∀ {ℓ} (A : Type ℓ)(B : Type ℓ) (α : A == B)(a : A)(b : B) → Type ℓ HEq₄ A .A idp a b = Path a b
Equivalences
The following equivalences are all provable by path-induction, we do path
induction on the path α from the definition above and depending on the
heterogeneous equality definition we chose we might be need other path
induction. The convention for the equivalences is HEqᵢ-≃-HEqⱼ to denote the
evidence of the equivalence between the type HEqᵢ and HEqⱼ.
Let us prove the equivalence between the types HEq₁ and HEq₂.
The other equivalences are proved in a similar way and they are available
on the website that supports this document.
-- HEq₁-≃-HEq₂ module _ {ℓ}(A : Type ℓ) (B : Type ℓ) where
-- Outgoing functions HEq₁-to-HEq₂ : {α : A == B}{a : A}{b : B} → HEq₁ A B α a b → HEq₂ A B α a b HEq₁-to-HEq₂ {idp} idp = idp HEq₂-to-HEq₁ : {α : A == B}{a : A}{b : B} → HEq₂ A B α a b → HEq₁ A B α a b HEq₂-to-HEq₁ {idp} idp = idp
Finally, we provide the evidence of the equivalence.
-- Equivalence HEq₁-≃-HEq₂ : {α : A == B}{a : A}{b : B} → HEq₁ A B α a b ≃ HEq₂ A B α a b HEq₁-≃-HEq₂ {idp} {a} {b} = qinv-≃ HEq₁-to-HEq₂ (HEq₂-to-HEq₁ , HEq₁-~-HEq₂ , HEq₂-~-HEq₁) where HEq₁-~-HEq₂ : ( p : HEq₂ A B idp a b) → ( HEq₁-to-HEq₂ (HEq₂-to-HEq₁ p ) == p) HEq₁-~-HEq₂ idp = idp HEq₂-~-HEq₁ : ( p : HEq₁ A B idp a b) → ( HEq₂-to-HEq₁ (HEq₁-to-HEq₂ p ) == p) HEq₂-~-HEq₁ idp = idp
-- Other equivalences: HEq₂-≃-HEq₃, HEq₃-≃-HEq₄, HEq₄-≃-HEq₁ -- HEq₂-≃-HEq₃ module _ {ℓ}(A : Type ℓ) (B : Type ℓ) where HEq₂-to-HEq₃ : {α : A == B}{a : A}{b : B} → HEq₂ A B α a b → HEq₃ A B α a b HEq₂-to-HEq₃ {idp} idp = idp HEq₃-to-HEq₂ : {α : A == B}{a : A}{b : B} → HEq₃ A B α a b → HEq₂ A B α a b HEq₃-to-HEq₂ {idp} idp = idp HEq₂-≃-HEq₃ : {α : A == B}{a : A}{b : B} → HEq₂ A B α a b ≃ HEq₃ A B α a b HEq₂-≃-HEq₃ {idp} {a} {b} = qinv-≃ HEq₂-to-HEq₃ (HEq₃-to-HEq₂ , HEq₂-~-HEq₃ , HEq₃-~-HEq₂) where HEq₂-~-HEq₃ : ( p : HEq₃ A B idp a b) → ( HEq₂-to-HEq₃ (HEq₃-to-HEq₂ p ) == p) HEq₂-~-HEq₃ idp = idp HEq₃-~-HEq₂ : ( p : HEq₂ A B idp a b) → ( HEq₃-to-HEq₂ (HEq₂-to-HEq₃ p ) == p) HEq₃-~-HEq₂ idp = idp -- HEq₃-≃-HEq₄ module _ {ℓ}(A : Type ℓ) (B : Type ℓ) where HEq₃-to-HEq₄ : {α : A == B}{a : A}{b : B} → HEq₃ A B α a b → HEq₄ A B α a b HEq₃-to-HEq₄ {idp} idp = idp HEq₄-to-HEq₃ : {α : A == B}{a : A}{b : B} → HEq₄ A B α a b → HEq₃ A B α a b HEq₄-to-HEq₃ {idp} idp = idp HEq₃-≃-HEq₄ : {α : A == B}{a : A}{b : B} → HEq₃ A B α a b ≃ HEq₄ A B α a b HEq₃-≃-HEq₄ {idp} {a} {b} = qinv-≃ HEq₃-to-HEq₄ (HEq₄-to-HEq₃ , HEq₃-~-HEq₄ , HEq₄-~-HEq₃) where HEq₃-~-HEq₄ : ( p : HEq₄ A B idp a b) → ( HEq₃-to-HEq₄ (HEq₄-to-HEq₃ p ) == p) HEq₃-~-HEq₄ idp = idp HEq₄-~-HEq₃ : ( p : HEq₃ A B idp a b) → ( HEq₄-to-HEq₃ (HEq₃-to-HEq₄ p ) == p) HEq₄-~-HEq₃ idp = idp -- HEq₄-≃-HEq₁ module _ {ℓ}(A : Type ℓ) (B : Type ℓ) where HEq₄-to-HEq₁ : {α : A == B}{a : A}{b : B} → HEq₄ A B α a b → HEq₁ A B α a b HEq₄-to-HEq₁ {idp} idp = idp HEq₁-to-HEq₄ : {α : A == B}{a : A}{b : B} → HEq₁ A B α a b → HEq₄ A B α a b HEq₁-to-HEq₄ {idp} idp = idp HEq₄-≃-HEq₁ : {α : A == B}{a : A}{b : B} → HEq₄ A B α a b ≃ HEq₁ A B α a b HEq₄-≃-HEq₁ {idp} {a} {b} = qinv-≃ HEq₄-to-HEq₁ (HEq₁-to-HEq₄ , HEq₄-~-HEq₁ , HEq₁-~-HEq₄) where HEq₄-~-HEq₁ : ( p : HEq₁ A B idp a b) → ( HEq₄-to-HEq₁ (HEq₁-to-HEq₄ p ) == p) HEq₄-~-HEq₁ idp = idp HEq₁-~-HEq₄ : ( p : HEq₄ A B idp a b) → ( HEq₁-to-HEq₄ (HEq₄-to-HEq₁ p ) == p) HEq₁-~-HEq₄ idp = idp
We prefer to use definition HEq₁ as the definition by default for
heterogeneous equality. We later on refer to this type as HEq.
HEq = HEq₂
Paths in the total space
As we mentioned above, Pathover can be defined in at least five different ways. An inductive definition, using the heterogeneous equality, transporting along homogeneous equalities and the last one by path-induction on the identity type.
-
data PathOver₁ {ℓᵢ ℓⱼ} {A : Set ℓᵢ} (C : A → Type ℓⱼ) {a₁ : A} : {a₂ : A} (α : a₁ == a₂) (c₁ : C a₁) (c₂ : C a₂) → Type (ℓᵢ ⊔ ℓⱼ) where idp : ∀ {c₁ : C a₁} → PathOver₁ C idp c₁ c₁
-
PathOver₂ : ∀ {ℓᵢ ℓⱼ} {A : Type ℓᵢ} → (C : A → Type ℓⱼ) {a₁ a₂ : A} → (α : a₁ == a₂) → (c₁ : C a₁) → (c₂ : C a₂) ------------------- → Type ℓⱼ PathOver₂ {A = A} C {a₁} {a₂} α c₁ c₂ = HEq (C a₁) (C a₂) (ap C α) c₁ c₂
-
PathOver₃ : ∀ {ℓᵢ ℓⱼ} {A : Type ℓᵢ} → (C : A → Type ℓⱼ) {a₁ a₂ : A} → (α : a₁ == a₂) → (c₁ : C a₁) → (c₂ : C a₂) ------------------- → Type ℓⱼ PathOver₃ C α c₁ c₂ = transport C α c₁ == c₂
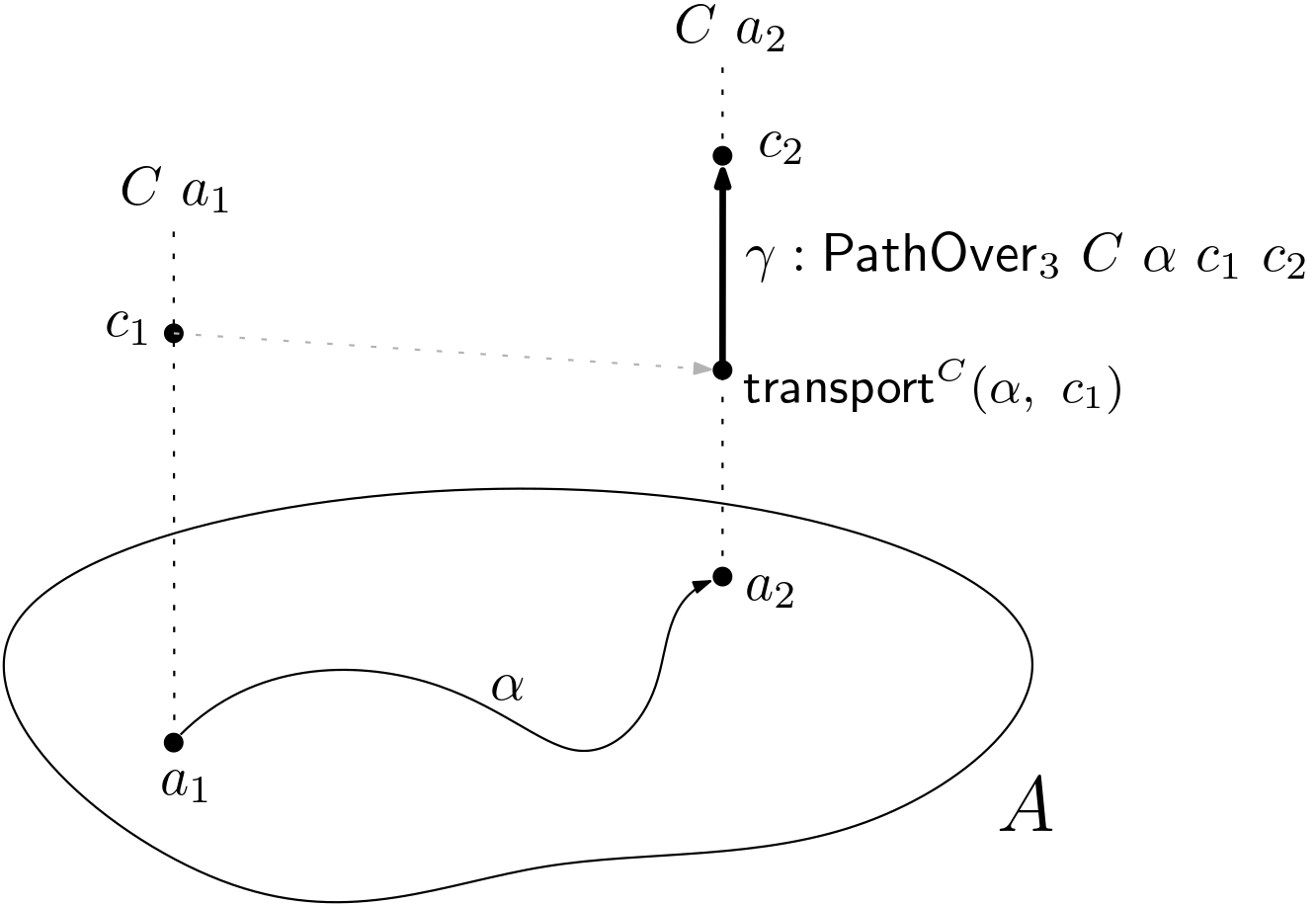 Figure 2. Pathover₃.
Figure 2. Pathover₃.
-
PathOver₄ : ∀ {ℓᵢ ℓⱼ} {A : Type ℓᵢ} → (C : A → Type ℓⱼ) {a₁ a₂ : A} → (α : a₁ == a₂) → (c₁ : C a₁) → (c₂ : C a₂) ------------------- → Type ℓⱼ PathOver₄ C α c₁ c₂ = c₁ == transport C (α ⁻¹) c₂
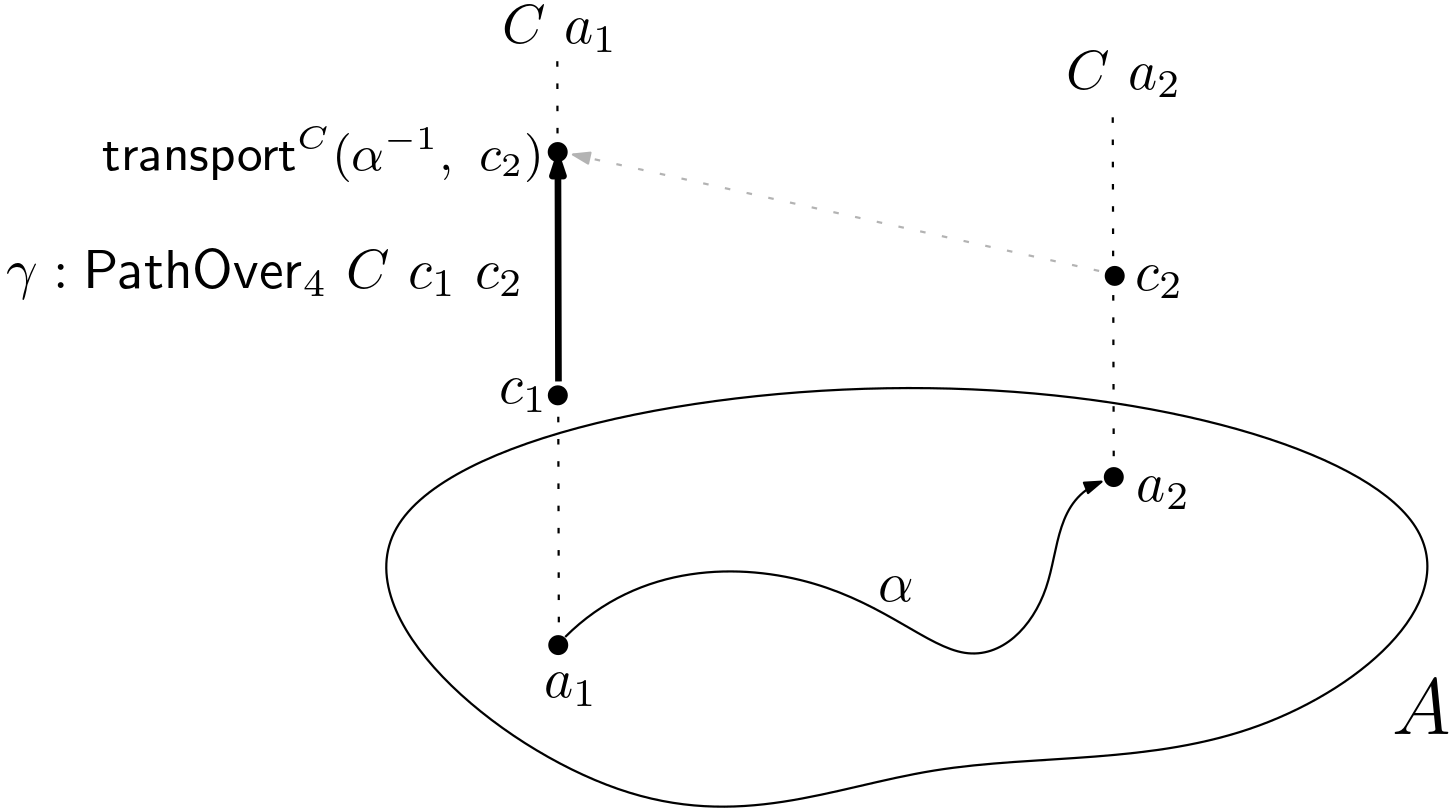 Figure 3. Pathover₄.
Figure 3. Pathover₄.
-
PathOver₅ : ∀ {ℓᵢ ℓⱼ} {A : Type ℓᵢ} → (C : A → Type ℓⱼ) {a₁ a₂ : A} → (α : a₁ == a₂) → (c₁ : C a₁) → (c₂ : C a₂) ------------------- → Type ℓⱼ PathOver₅ _ idp c₁ c₂ = c₁ == c₂
Equivalences
The following equivalences are all provable by path-induction, we do path
induction on the path α from the definition above and depending on the
heterogeneous equality definition we chose we might be need other path
induction. The convention for the equivalences is PathOverᵢ-≃-PathOverⱼ to
denote the evidence of the equivalence between the type PathOverᵢ and
PathOverⱼ.
Let us prove the equivalence between the types PathOver₁ and PathOver₂.
The other equivalences are proved in a similar way but they are available
on the website of this document.
-- PathOver₁-≃-PathOver₂ module _ {ℓ} (A : Type ℓ) (C : A → Type ℓ) where -- Outgoing functions PathOver₁-to-PathOver₂ : ∀ {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂} → PathOver₁ C α c₁ c₂ → PathOver₂ C α c₁ c₂ PathOver₁-to-PathOver₂ {α = idp} idp = idp PathOver₂-to-PathOver₁ : ∀ {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂} → PathOver₂ C α c₁ c₂ → PathOver₁ C α c₁ c₂ PathOver₂-to-PathOver₁ {α = idp} idp = idp
Finally, we provide the evidence of the equivalence.
-- Equivalence PathOver₁-≃-PathOver₂ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂} → PathOver₁ C α c₁ c₂ ≃ PathOver₂ C α c₁ c₂ PathOver₁-≃-PathOver₂ {α = idp}{c₁}{c₂} = qinv-≃ PathOver₁-to-PathOver₂ (PathOver₂-to-PathOver₁ , PathOver₁~PathOver₂ , PathOver₂~PathOver₁) where PathOver₁~PathOver₂ : (p : PathOver₂ C idp c₁ c₂) → PathOver₁-to-PathOver₂ (PathOver₂-to-PathOver₁ p) == p PathOver₁~PathOver₂ idp = idp PathOver₂~PathOver₁ : (p : PathOver₁ C idp c₁ c₂) → PathOver₂-to-PathOver₁ (PathOver₁-to-PathOver₂ p) == p PathOver₂~PathOver₁ idp = idp
-- Other equivalences: -- PathOver₂-≃-PathOver₃, PathOver₃-≃-PathOver₄, PathOver₄-≃-PathOver₅, PathOver₁-≃-PathOver₁ -- PathOver₂-≃-PathOver₃ module _ {ℓ} (A : Type ℓ) (C : A → Type ℓ) where PathOver₂-to-PathOver₃ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂} → PathOver₂ C α c₁ c₂ → PathOver₃ C α c₁ c₂ PathOver₂-to-PathOver₃ {α = idp} idp = idp PathOver₃-to-PathOver₂ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂} → PathOver₃ C α c₁ c₂ → PathOver₂ C α c₁ c₂ PathOver₃-to-PathOver₂ {α = idp} idp = idp PathOver₂-≃-PathOver₃ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂} → PathOver₂ C α c₁ c₂ ≃ PathOver₃ C α c₁ c₂ PathOver₂-≃-PathOver₃ {α = idp}{c₁}{c₂} = qinv-≃ PathOver₂-to-PathOver₃ (PathOver₃-to-PathOver₂ , PathOver₂~PathOver₃ , PathOver₃~PathOver₂) where PathOver₂~PathOver₃ : (p : PathOver₃ C idp c₁ c₂) → PathOver₂-to-PathOver₃ (PathOver₃-to-PathOver₂ p) == p PathOver₂~PathOver₃ idp = idp PathOver₃~PathOver₂ : (p : PathOver₂ C idp c₁ c₂) → PathOver₃-to-PathOver₂ (PathOver₂-to-PathOver₃ p) == p PathOver₃~PathOver₂ idp = idp -- PathOver₃-≃-PathOver₄ module _ {ℓ} (A : Type ℓ) (C : A → Type ℓ) where PathOver₃-to-PathOver₄ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂} → PathOver₃ C α c₁ c₂ → PathOver₄ C α c₁ c₂ PathOver₃-to-PathOver₄ {α = idp} idp = idp PathOver₄-to-PathOver₃ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂} → PathOver₄ C α c₁ c₂ → PathOver₃ C α c₁ c₂ PathOver₄-to-PathOver₃ {α = idp} idp = idp PathOver₃-≃-PathOver₄ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂} → PathOver₃ C α c₁ c₂ ≃ PathOver₄ C α c₁ c₂ PathOver₃-≃-PathOver₄ {α = idp}{c₁}{c₂} = qinv-≃ PathOver₃-to-PathOver₄ (PathOver₄-to-PathOver₃ , PathOver₃~PathOver₄ , PathOver₄~PathOver₃) where PathOver₃~PathOver₄ : (p : PathOver₄ C idp c₁ c₂) → PathOver₃-to-PathOver₄ (PathOver₄-to-PathOver₃ p) == p PathOver₃~PathOver₄ idp = idp PathOver₄~PathOver₃ : (p : PathOver₃ C idp c₁ c₂) → PathOver₄-to-PathOver₃ (PathOver₃-to-PathOver₄ p) == p PathOver₄~PathOver₃ idp = idp -- PathOver₄-≃-PathOver₅ module _ {ℓ} (A : Type ℓ) (C : A → Type ℓ) where PathOver₄-to-PathOver₅ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂} → PathOver₄ C α c₁ c₂ → PathOver₅ C α c₁ c₂ PathOver₄-to-PathOver₅ {α = idp} idp = idp PathOver₅-to-PathOver₄ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂} → PathOver₅ C α c₁ c₂ → PathOver₄ C α c₁ c₂ PathOver₅-to-PathOver₄ {α = idp} idp = idp PathOver₄-≃-PathOver₅ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂} → PathOver₄ C α c₁ c₂ ≃ PathOver₅ C α c₁ c₂ PathOver₄-≃-PathOver₅ {α = idp}{c₁}{c₂} = qinv-≃ PathOver₄-to-PathOver₅ (PathOver₅-to-PathOver₄ , PathOver₄~PathOver₅ , PathOver₅~PathOver₄) where PathOver₄~PathOver₅ : (p : PathOver₅ C idp c₁ c₂) → PathOver₄-to-PathOver₅ (PathOver₅-to-PathOver₄ p) == p PathOver₄~PathOver₅ idp = idp PathOver₅~PathOver₄ : (p : PathOver₄ C idp c₁ c₂) → PathOver₅-to-PathOver₄ (PathOver₄-to-PathOver₅ p) == p PathOver₅~PathOver₄ idp = idp -- PathOver₅-≃-PathOver₁ module _ {ℓ} (A : Type ℓ) (C : A → Type ℓ) where PathOver₅-to-PathOver₁ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂} → PathOver₅ C α c₁ c₂ → PathOver₁ C α c₁ c₂ PathOver₅-to-PathOver₁ {α = idp} idp = idp PathOver₁-to-PathOver₅ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂} → PathOver₁ C α c₁ c₂ → PathOver₅ C α c₁ c₂ PathOver₁-to-PathOver₅ {α = idp} idp = idp PathOver₅-≃-PathOver₁ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂} → PathOver₅ C α c₁ c₂ ≃ PathOver₁ C α c₁ c₂ PathOver₅-≃-PathOver₁ {α = idp}{c₁}{c₂} = qinv-≃ PathOver₅-to-PathOver₁ (PathOver₁-to-PathOver₅ , PathOver₅~PathOver₁ , PathOver₁~PathOver₅) where PathOver₅~PathOver₁ : (p : PathOver₁ C idp c₁ c₂) → PathOver₅-to-PathOver₁ (PathOver₁-to-PathOver₅ p) == p PathOver₅~PathOver₁ idp = idp PathOver₁~PathOver₅ : (p : PathOver₅ C idp c₁ c₂) → PathOver₁-to-PathOver₅ (PathOver₅-to-PathOver₁ p) == p PathOver₁~PathOver₅ idp = idp
By default, we use the third definition because it is the same definition used in (Univalent Foundations Program, 2013) in Section 2.3. The syntax sugar for pathovers is used in (Brunerie et al., 2018).
PathOver = PathOver₃ infix 30 PathOver syntax PathOver C α c₁ c₂ = c₁ == c₂ [ C ↓ α ]
Total spaces
Theorem
Let be A : Type, a path α : a₁ == a₂ of two terms a₁, a₂ : A and a type
family C : A → Type. If c₁ : C a₁ and c₂ : C a₂ then the type of the
pathovers between c₁ and c₁ over the path α is equivalent to the sigma
type of (a₁ , c₁) == (a₂ , c₂) such that ap π₁ q == α, that is the following
equivalence,
Proof.
module _ {ℓᵢ ℓⱼ}{A : Type ℓᵢ}{C : A → Type ℓⱼ}{a₁ a₂ : A} where
We prove this equivalence by the quasi-inverse function Σ-to-==[↓]. Therefore,
we define its inverse, the function ==[↓]-to-Σ and we show the respective
homotopies, Σ-to-==[↓] ∘ ==[↓]-to-Σ ~ id and ==[↓]-to-Σ ∘ Σ-to-==[↓] ~ id.
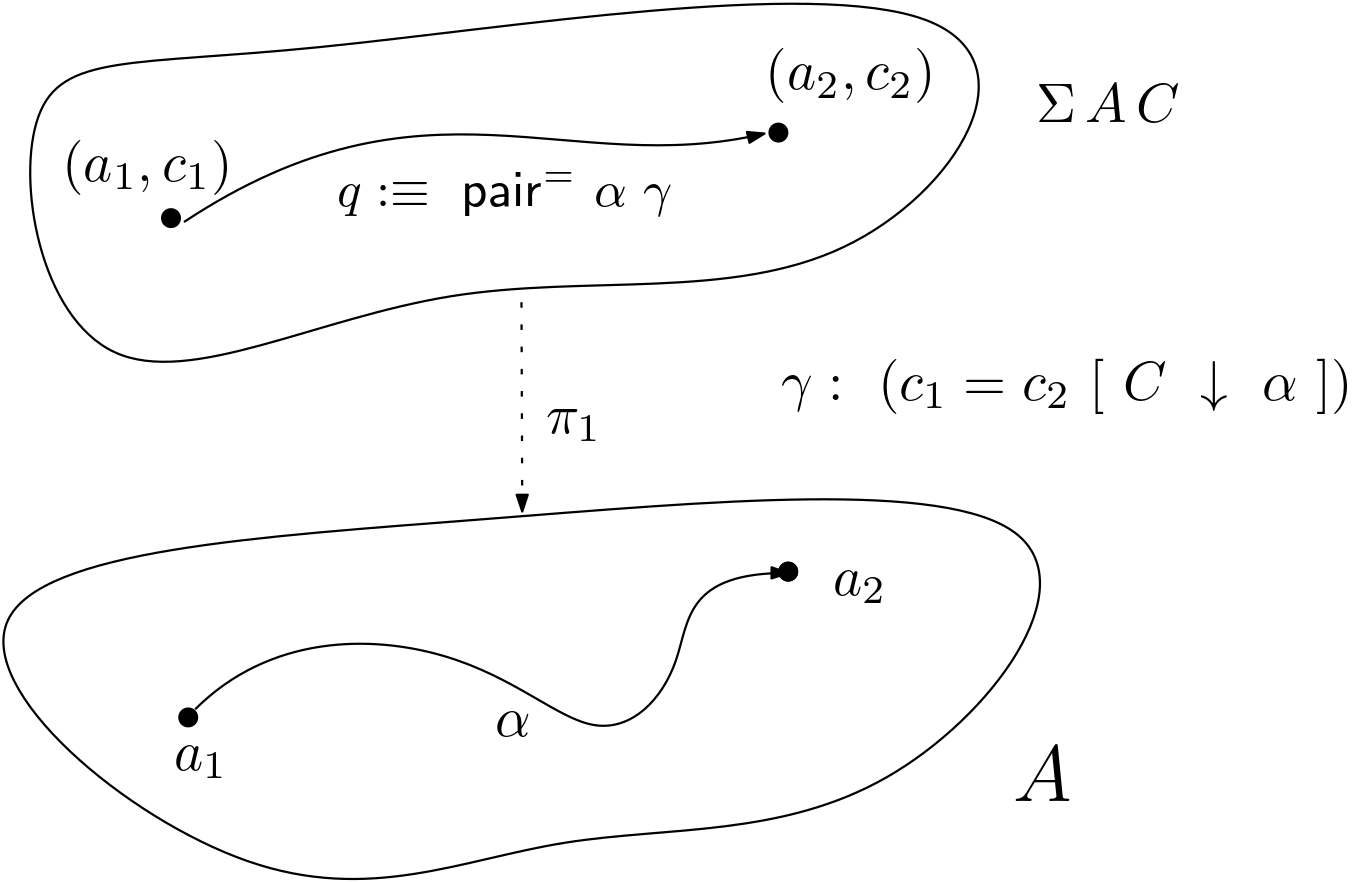 Figure 4. Pathovers and paths in the total space.
Figure 4. Pathovers and paths in the total space.
- The function
Σ-to-==[↓]maps a term of the sigma type in the equation above to the pathoverc₁ == c₂ [ C ↓ α ]. In its construction, we use Σ-induction followed by two path-inductions on each of the its sigma components. As result, we only have to provide a term of the identity typec₁ == c₂wherec₁andc₂are judgementally equal, which isidp.
-- Def. Σ-to-==[↓] : {α : a₁ == a₂}{c₁ : C a₁}{c₂ : C a₂} → Σ ((a₁ , c₁) == (a₂ , c₂)) (λ q → (ap π₁ q) == α) → c₁ == c₂ [ C ↓ α ] Σ-to-==[↓] (idp , idp) = idp
- The respective inverse function is
==[↓]-to-Σ, which maps terms of the pathoverc₁ == c₂ [ C ↓ α ]to pairs inΣ ((a₁ , c₁) == (a₂ , c₂)) (λ q → (ap π₁ q) == α). In its construction, we use path-induction on the pathαin the base space follows by the induction on the pathoverγ. As result, we define this function as a pair of reflexivity proofs.
-- Def. ==[↓]-to-Σ : {α : a₁ == a₂}{c₁ : C a₁}{c₂ : C a₂} → (γ : c₁ == c₂ [ C ↓ α ]) → Σ ((a₁ , c₁) == (a₂ , c₂)) (λ q → (ap π₁ q) == α) ==[↓]-to-Σ {idp} idp = (idp , idp)
Remark. We could also have defined the above function by using the pair= function
which is the right-left direction in Theorem 2.7.2 in (Univalent Foundations Program, 2013) and
the function ap-π₁-pair= that maps a path α in the base space and the
pathover γ to a term m of type ap π₁ (pair= (α , γ)) == α.
That is, ==[↓]-to-Σ α γ = (pair= α γ, m).
However, we do not get any benefit as far as we know of the latter definition
against the former definition and therefore, we have preferred the former which
is simpler, elegant and exploits the pattern matching of Agda as well as in the
following homotopies.
-- Homotopy: Σ-to-==[↓] ∘ ==[↓]-to-Σ ~ id private H₁ : {α : a₁ == a₂}{c₁ : C a₁}{c₂ : C a₂} → (γ : c₁ == c₂ [ C ↓ α ]) → Σ-to-==[↓] {α = α} (==[↓]-to-Σ γ) == γ H₁ {α = idp} idp = idp
-- Homotopy: ==[↓]-to-Σ ∘ Σ-to-==[↓] ∼ id private H₂ : {α : a₁ == a₂}{c₁ : C a₁}{c₂ : C a₂} → (pair : Σ ((a₁ , c₁) == (a₂ , c₂)) (λ q → (ap π₁ q) == α)) → ==[↓]-to-Σ (Σ-to-==[↓] pair) == pair H₂ (idp , idp) = idp
Our remaining step now is to show the respective equivalence. To show that, we
have used the function qinv-≃ that provides us a way to convert a
quasi-inverse function into the equivalence between its domain and codomain.
Since the function Σ-to-==[↓] is quasi-inverse by definition using ==[↓]-to-Σ,
H₁ and H₂ hence the equivalence follows.
-- Equivalence private Σ-≃-==[↓] : {α : a₁ == a₂}{c₁ : C a₁}{c₂ : C a₂} → (Σ ((a₁ , c₁) == (a₂ , c₂)) (λ q → (ap π₁ q) == α)) ≃ (c₁ == c₂ [ C ↓ α ]) Σ-≃-==[↓] = qinv-≃ Σ-to-==[↓] -- the quasi-inverse ( ==[↓]-to-Σ -- its inverse , H₁ -- homotopy: Σ-to-==[↓] ∘ ==[↓]-to-Σ ~ id , H₂ -- homotopy: ==[↓]-to-Σ ∘ Σ-to-==[↓] ∼ id )
In the remaining of this section, we prove some useful results about sigma types that allow us to give a shorter proof of the equivalence proved above.
Lemma 1
If and and , then
Proof.
Our context:
module Lemma₁ {ℓᵢ}{ℓⱼ} {A : Type ℓᵢ} {B : Type ℓᵢ} (e : B ≃ A) {C : A → Type ℓⱼ} where
We extract the functions and the homotopies from the equivalence e : B ≃ A
to use them later.
-- Def. private f : B → A f = lemap e ishaef : ishae f ishaef = ≃-ishae e f⁻¹ : A → B f⁻¹ = ishae.g ishaef α : f ∘ f⁻¹ ∼ id α = ishae.ε ishaef β : f⁻¹ ∘ f ∼ id β = ishae.η ishaef τ : (b : B) → ap f (β b) == α (f b) τ = ishae.τ ishaef
Now, we proceed to define the outgoing functions from to and conversely.
-- Def. ΣAC-to-ΣBCf : Σ A C → Σ B (λ b → C (f b)) ΣAC-to-ΣBCf (a , c) = f⁻¹ a , c' where c' : C (f (f⁻¹ a)) c' = transport C ((α a) ⁻¹) c
-- Def. ΣBCf-to-ΣAC : Σ B (λ b → C (f b)) → Σ A C ΣBCf-to-ΣAC (b , c') = f b , c'
Evidence of the homotopies necessary to show the equivalence:
-- Homotopies private H₁ : ΣAC-to-ΣBCf ∘ ΣBCf-to-ΣAC ∼ id H₁ (b , c') = pair= (β b , patho) where c'' : C (f (f⁻¹ (f b))) c'' = transport C ((α (f b)) ⁻¹) c' -- patho : c'' == c' [ (C ∘ f) ↓ (β b)] patho : transport (λ x → C (f x)) (β b) c'' == c' patho = begin transport (λ x → C (f x)) (β b) c'' ==⟨ transport-family (β b) c'' ⟩ transport C (ap f (β b)) c'' ==⟨ ap (λ γ → transport C γ c'') (τ b) ⟩ transport C (α (f b)) c'' ==⟨ transport-comp-h ((α (f b)) ⁻¹) (α (f b)) c' ⟩ transport C ( ((α (f b)) ⁻¹) · α (f b)) c' ==⟨ ap (λ γ → transport C γ c') (·-linv (α (f b))) ⟩ transport C idp c' ==⟨⟩ c' ∎ private H₂ : ΣBCf-to-ΣAC ∘ ΣAC-to-ΣBCf ∼ id H₂ (a , c) = pair= (α a , patho) where patho : transport C (α a) (transport C ((α a) ⁻¹) c) == c patho = begin transport C (α a) (transport C ((α a) ⁻¹) c) ==⟨ transport-comp-h (((α a) ⁻¹)) (α a) c ⟩ transport C ( ((α a) ⁻¹) · (α a) ) c ==⟨ ap (λ γ → transport C γ c) (·-linv (α a)) ⟩ transport C idp c ==⟨⟩ c ∎
Finally, we now are able to prove the equivalence using the terms defined above.
-- Equivalence lemma₁ : Σ A C ≃ Σ B (λ b → C (f b)) lemma₁ = qinv-≃ ΣAC-to-ΣBCf -- the quasi-inverse ( ΣBCf-to-ΣAC -- its inverse , H₁ -- ΣAC-to-ΣBCf ∘ ΣBCf-to-ΣAC ∼ id , H₂ -- ΣBCf-to-ΣAC ∘ ΣAC-to-ΣBCf ∼ id ) open Lemma₁ public
Lemma 2
If and and then
Proof.
module Lemma₂ {ℓ} {A : Type ℓ}{C : A → Type ℓ}(a : A) where ΣΣ-to-C : Σ (Σ A C) (λ w → π₁ w == a) → C a ΣΣ-to-C ((a , c) , p) = transport C p c C-to-ΣΣ : C a → Σ (Σ A C) (λ w → π₁ w == a) C-to-ΣΣ c = (a , c) , idp private H₁ : ΣΣ-to-C ∘ C-to-ΣΣ ∼ id H₁ c = idp H₂ : C-to-ΣΣ ∘ ΣΣ-to-C ∼ id H₂ ((a' , c) , p) = pair= (paireq , patho) where c' : transport C (inv p) (transport C p c) == c c' = begin transport C (inv p) (transport C p c) ==⟨ transport-comp-h p ((inv p)) c ⟩ transport C (p · (inv p)) c ==⟨ ap (λ γ → transport C γ c) (·-rinv p) ⟩ transport C idp c ==⟨⟩ c ∎ paireq : a , transport C p c == a' , c paireq = pair= (inv p , c') patho : transport (λ w → π₁ w == a) paireq idp == p patho = begin transport (λ w → π₁ w == ((λ _ → a) w)) paireq idp ==⟨ transport-eq-fun π₁ (λ _ → a) paireq idp ⟩ inv (ap π₁ paireq) · idp · ap (λ _ → a) paireq ==⟨ ap (λ γ → inv (ap π₁ paireq) · idp · γ) (ap-const paireq) ⟩ inv (ap π₁ paireq) · idp · idp ==⟨ ·-runit-infer ⟩ inv (ap π₁ paireq) · idp ==⟨ ·-runit-infer ⟩ inv (ap π₁ paireq) ==⟨ ap (λ p → inv p) (ap-π₁-pair= (inv p) c') ⟩ inv (inv p) ==⟨ involution ⟩ p ∎ lemma₂ : Σ (Σ A C) (λ w → π₁ w == a) ≃ C a lemma₂ = qinv-≃ ΣΣ-to-C (C-to-ΣΣ , H₁ , H₂) open Lemma₂ public
Lemma 3
If and for two type families . If we have , then
Proof.
module Lemma₃ {ℓ} {A : Type ℓ}{C : A → Type ℓ}{D : A → Type ℓ} (e : (a : A) → C a ≃ D a) where private f : (a : A) → C a → D a f a = lemap (e a) f⁻¹ : (a : A) → D a → C a f⁻¹ a = remap (e a) α : (a : A) → (f a) ∘ (f⁻¹ a) ∼ id α a x = lrmap-inverse (e a) β : (a : A) → (f⁻¹ a) ∘ (f a) ∼ id β a x = rlmap-inverse (e a) ΣAC-to-ΣAD : Σ A C → Σ A D ΣAC-to-ΣAD (a , c) = (a , (f a) c) ΣAD-to-ΣAC : Σ A D → Σ A C ΣAD-to-ΣAC (a , d) = (a , (f⁻¹ a) d) H₁ : ΣAC-to-ΣAD ∘ ΣAD-to-ΣAC ∼ id H₁ (a , d) = pair= (idp , α a d) H₂ : ΣAD-to-ΣAC ∘ ΣAC-to-ΣAD ∼ id H₂ (a , c) = pair= (idp , β a c) lemma₃ : Σ A C ≃ Σ A D lemma₃ = qinv-≃ ΣAC-to-ΣAD (ΣAD-to-ΣAC , H₁ , H₂) open Lemma₃ public
Alternative proof
Let us recall the equivalence.
where , , and .
Using the previous lemmas, the following is an alternative proof of the theorem
Σ-≃-==[↓].
Proof.
Our context for this proof:
module _ {ℓ} {A : Type ℓ} {C : A → Type ℓ} {a₁ a₂ : A} (α : a₁ == a₂) {c₁ : C a₁} {c₂ : C a₂} where
-- Theorem. private Σ-≃-==[↓] : Σ ((a₁ , c₁) == ( a₂ , c₂)) (λ q → ap π₁ q == α) ≃ PathOver C α c₁ c₂ Σ-≃-==[↓] = begin≃ Σ ((a₁ , c₁) == ( a₂ , c₂)) (λ q → ap π₁ q == α) ≃⟨ lemma₁ pair=Equiv ⟩ Σ (Σ (a₁ == a₂) (λ β → transport C β c₁ == c₂)) (λ γ → ap π₁ (pair= γ) == α) ≃⟨ lemma₃ (ap-π₁-pair=Equiv α) ⟩ Σ (Σ (a₁ == a₂) (λ β → transport C β c₁ == c₂)) (λ γ → π₁ γ == α) ≃⟨ lemma₂ α ⟩ transport C α c₁ == c₂ ≃⟨⟩ PathOver C α c₁ c₂ ≃∎
Agda Libraries
We based on the following Agda libraries.
-
Pathovers: https://github.com/HoTT/HoTT-Agda/.
-
Basic homotopy type theory in Agda: agda-hott.
- Brunerie, G., Hou (Favonia), K.-B., Cavallo, E., Finster, E., Cockx, J., Sattler, C., … Others. (2018). Homotopy Type Theory in Agda. Retrieved from https://github.com/HoTT/HoTT-Agda
- Licata, D. R., & Brunerie, G. (2015). A cubical approach to synthetic homotopy theory. Proceedings - Symposium on Logic in Computer Science, 2015-July, 92–103. https://doi.org/10.1109/LICS.2015.19
- Univalent Foundations Program, T. (2013). Homotopy Type Theory: Univalent Foundations of Mathematics. Institute for Advanced Study. Retrieved from http://saunders.phil.cmu.edu/book/hott-online.pdf