Pathovers

Jonathan Prieto-Cubides

University of Bergen

Marc Bezem

University of Bergen

05 July 2018

No git information available.

Pathovers

Javascript is disabled, please activate it to see correctly this post.

This is a work in progress jointly with Marc Bezem. Some of the following proofs are collapsed or hidden to reduce the size of the document. Nevertheless, the reader can click on them to open the full description. Pictures are also clickable.

Introduction

The type of pathovers can be defined in at least five different ways, all equivalent as we show later in this document (see also (Licata & Brunerie, 2015)).

Let A : Type, a₁, a₂ : A, C : A → Type, c₁ : C a₁ and c₂ : C a₂. Using the same notation from (Univalent Foundations Program, 2013), one of the definitions for the Pathover type is as the shorthand for the path between the transport along a path α : a₁ = a₂ of the point c₁ : C a₁ and the point c₂ in the fiber C a₂. That is, a pathover is a term that inhabits the type (transport C α c₁) = c₂ also denoted by PathOver C α c₁ c₂.

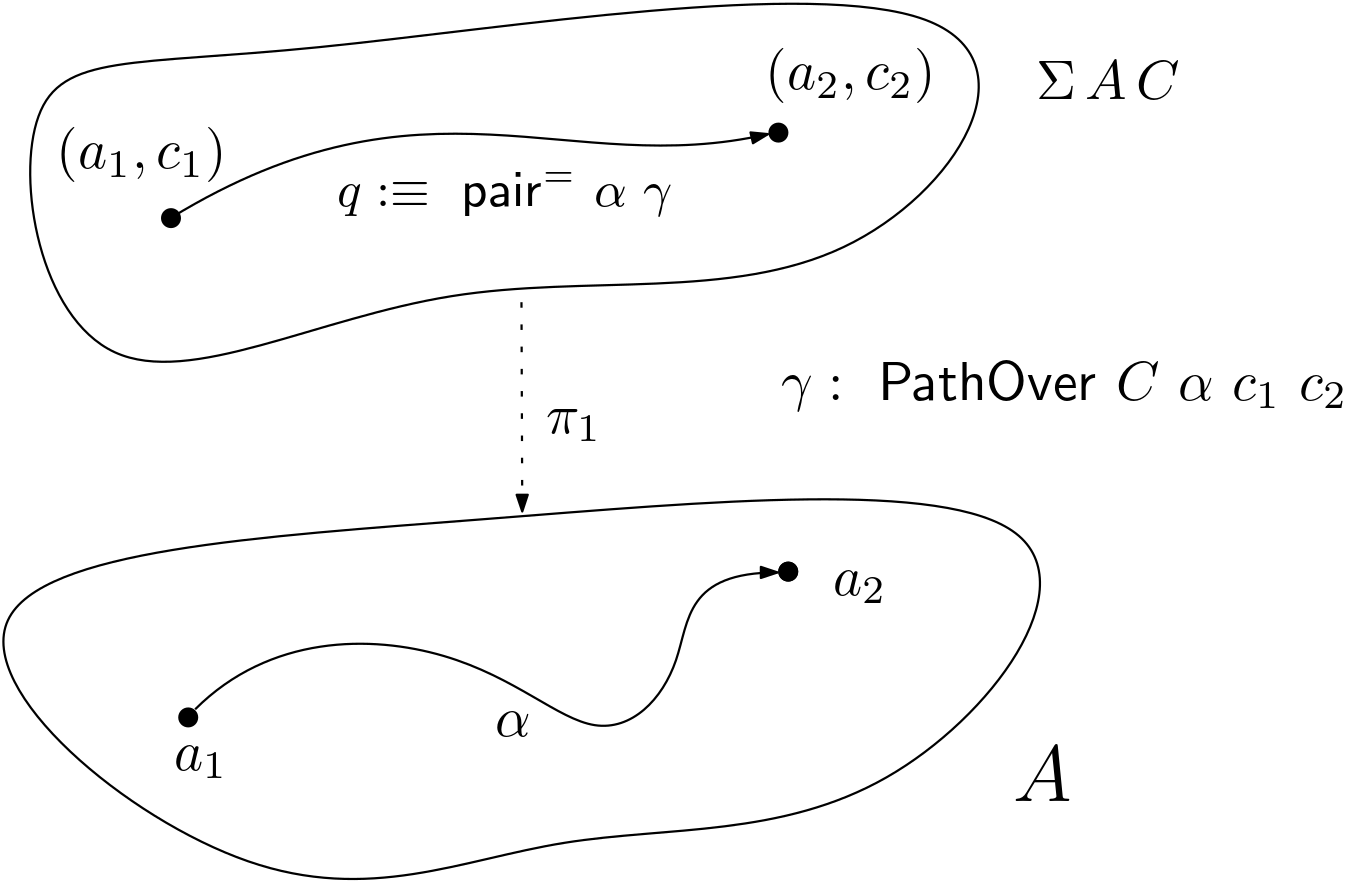path Figure 1. PathOvers and paths in the total space.

The term pathover was formally defined in (Licata & Brunerie, 2015) and also briefly mentioned in Section 2.3 in (Univalent Foundations Program, 2013) as a path in the total space of C which “lies over” α.

We are interested to prove the geometrical intuition behind these pathovers in which the path q : (a₁, c₁) = (a₂, c₂) is projected down onto α : a₁ = a₂ as it follows from the figure showed above. Σ A C is the total space and “projecting down” means ap π₁ q = α where π₁ : Σ A C → A.

We formalize such a correspondence by showing the following equivalence,

$\sum\limits_{q : (a₁ , c₁) = (a₂ , c₂)} \ (\mathsf{ap}~\mathsf{\pi_{1}}~q~= \alpha) \simeq \mathsf{PathOver}~C~\alpha~c₁~c₂.$

We give two proofs of this equivalence. The second proof uses some results about Σ-types that make the second proof of the equivalence a little shorter. We also believe they can be useful in other contexts.

The correctness of this development has been type-checked by Agda v2.5.4. To be consistent with homotopy type theory, we tell Agda to not use Axiom K for type-checking by using the option without-K. Without Axiom K, Agda’s Set is not a good name for universes in HoTT and we rename Set to Type.


{-# OPTIONS --without-K #-}

open import Agda.Primitive using ( Level ; lsuc; _⊔_ )

Type : (ℓ : Level) → Set (lsuc ℓ)
Type ℓ = Set ℓ

Now, let us define in Agda the homogeneous equality type and the heterogeneous equality in order to define in different ways the PathOver type.

Homogeneous equality

The homogeneous equality is the Identity type denoted by Path that relates two elements a₀ and a₁ whose types are definitionally/judgmentally equal. We also refer to this type as a₁ == a₂ or Path a₁ a₂.

infix 30 _==_
data _==_ {ℓᵢ} {A : Type ℓᵢ} (a : A) : A → Type ℓᵢ where
  idp : a == a

Path = _==_

Heterogeneous equality

The heterogeneous equality as it is defined in (Licata & Brunerie, 2015) is a type for equality between two elements a : A, b : B, along an equality α : A == B. Its terms are constructed by the reflexivity constructor which applies only when both the two types and the two terms are judgementally equal.

We define in Agda the heterogeneous equality as HEq with a different subindex for each definition. We start with the inductive definition HEq₁ in the following.

data HEq₁ {ℓ} (A : Type ℓ)
            : (B : Type ℓ)
            → (α : A == B) (a : A) (b : B)
            → Type (lsuc ℓ) where
  idp : ∀ {a : A} → HEq₁ A A idp a a

In this definition, the reflexivity constructor for Paths is the same name as the constructor for homogeneous equality. Using the same name will allow us to switch between different definitions of heterogeneous equality in the posteriori proofs and also to switch between the definitions of the Pathover type.

Now, we have two types HEq₂ and HEq₃ that use the transport and the coercion functions, defined below. To define transport we do path-induction on the homogeneous equality between the terms and to define coercion (coe) we use transport. It is also possible to define them in the other way around, that is, transport by using coe.

transport
  : ∀ {ℓᵢ ℓⱼ} {A : Type ℓᵢ} (C : A → Type ℓⱼ) {a b : A}
  → a == b
  → C a
  → C b
transport C idp = (λ x → x)

coe
  : ∀ {ℓ}{A B : Type ℓ}
  → A == B
  → (A → B)
coe p A = transport (λ X → X) p A

--- Basic HoTT types, functions and theorems.

module hott where

  infixr 60 _,_
  record Σ {ℓᵢ ℓⱼ} (A : Type ℓᵢ)(C : A → Type ℓⱼ) : Type (ℓᵢ ⊔ ℓⱼ) where
    constructor _,_
    field
      π₁ : A
      π₂ : C π₁
  open Σ public

  Π : ∀ {ℓᵢ ℓⱼ} (A : Type ℓᵢ) (P : A → Type ℓⱼ) → Type (ℓᵢ ⊔ ℓⱼ)
  Π A P = (x : A) → P x

  _×_ : ∀{ℓᵢ ℓⱼ} (S : Type ℓᵢ) (T : Type ℓⱼ) → Type (ℓᵢ ⊔ ℓⱼ)
  A × B = Σ A (λ _ → B)

  infixr 80 _+_
  data _+_ {ℓᵢ ℓⱼ} (S : Type ℓᵢ) (T : Type ℓⱼ) : Type (ℓᵢ ⊔ ℓⱼ) where
    inl : S → S + T
    inr : T → S + T

  id : ∀ {ℓ} {A : Type ℓ} → A → A
  id a = a

  infixr 80 _∘_
  _∘_ : ∀{ℓᵢ ℓⱼ ℓₖ}
      {A : Type ℓᵢ}
      {B : A → Type ℓⱼ}
      {C : (a : A) → (B a → Type ℓₖ)}
      → (g : {a : A} → Π (B a) (C a)) → (f : Π A B) → Π A (λ a → C a (f a))
  g ∘ f = λ x → g (f x)

  infixr 0 _$_
  _$_ : ∀ {i j} {A : Type i} {B : A → Type j}
      → (∀ x → B x) → (∀ x → B x)
  f $ x = f x

  infixl 50 _·_
  _·_ : ∀ {ℓ} {A : Type ℓ}  {a b c : A} → a == b → b == c → a == c
  idp · q = q

  inv : ∀{ℓ} {A : Type ℓ}  {a b : A} → a == b → b == a
  inv idp = idp

  _⁻¹ = inv

  ap : ∀{ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ}  {a b : A} → (f : A → B)
    →   a == b
    → f a == f b
  ap f idp = idp

  module EquationalReasoning {ℓᵢ} {A : Type ℓᵢ} where

    infixr 2 _==⟨⟩_
    _==⟨⟩_ : ∀ (x {y} : A) → x == y → x == y
    _ ==⟨⟩ p = p

    infixr 2 _==⟨_⟩_
    _==⟨_⟩_ :  (x : A) {y z : A} → x == y → y == z → x == z
    _ ==⟨ p1 ⟩ p2 = p1 · p2

    infix  3 _∎
    _∎ : (x : A) → x == x
    _∎ = λ x → idp

    infix  1 begin_
    begin_ : {x y : A} → x == y → x == y
    begin_ p = p

  open EquationalReasoning public

  module ·-Properties {ℓ} {A : Type ℓ} where

    involution : {a b : A} {p : a == b} → inv (inv p) == p
    involution {p = idp} = idp

    ·-runit : {a b : A} (p : a == b) → p == p · idp
    ·-runit idp = idp

    ·-runit-infer : {a b : A} {p : a == b} →  p · idp == p
    ·-runit-infer {p = idp} = idp

    ·-lunit : {a b : A} (p : a == b) → p == idp · p
    ·-lunit idp = idp

    ·-assoc : {a b c d : A} (p : a == b) → (q : b == c) → (r : c == d)
            → (p · q) · r == p · (q · r)
    ·-assoc idp q r = idp

    ·-linv : {a b : A} (p : a == b) → (inv p) · p == idp
    ·-linv idp = idp

    ·-rinv : {a b : A} (p : a == b) → p · (inv p) == idp
    ·-rinv idp = idp

    ·-cancellation : {a : A} (p : a == a) → (q : a == a) → p · q == p → q == idp
    ·-cancellation {a} p q α =
      begin
        q                   ==⟨ ap (_· q) (inv (·-linv p)) ⟩
        inv p · p · q       ==⟨ (·-assoc (inv p) _ _) ⟩
        inv p · (p · q)     ==⟨ (ap (inv p ·_) α) ⟩
        inv p · p           ==⟨ ·-linv p ⟩
        idp
      ∎
  open ·-Properties public

  module Transport-Properties {ℓᵢ} {A : Type ℓᵢ} where

    -- Some lemmas on the transport operation.

    transport-const : ∀ {ℓⱼ} {P : A → Type ℓⱼ} {x y : A}
      {B : Type ℓᵢ}
      → (p : x == y)
      → (b : B)
      → transport (λ _ → B) p b == b
    transport-const idp _ = idp

    transport-concat-r : {a : A} {x y : A} → (p : x == y) → (q : a == x) →
      transport (λ x → a == x) p q == q · p
    transport-concat-r idp q = ·-runit q

    transport-concat-l : {a : A} {x y : A} → (p : x == y) → (q : x == a) →
      transport (λ x → x == a) p q == (inv p) · q
    transport-concat-l idp q = idp

    transport-concat : {x y : A} → (p : x == y) → (q : x == x) →
      transport (λ x → x == x) p q == (inv p) · q · p
    transport-concat idp q = ·-runit q

    transport-eq-fun : ∀{ℓⱼ} {B : Type ℓⱼ} (f g : A → B) {x y : A} (p : x == y) (q : f x == g x)
                      → transport (λ z → f z == g z) p q == inv (ap f p) · q · (ap g p)
    transport-eq-fun f g idp q = ·-runit q

    transport-comp : ∀{ℓⱼ} {a b c : A} {P : A → Type ℓⱼ} (p : a == b) (q : b == c)
                     → ((transport P q) ∘ (transport P p)) == transport P (p · q)
    transport-comp {P = P} idp q = idp {a = (transport P q)}

    transport-comp-h : ∀{ℓⱼ} {a b c : A} {P : A → Type ℓⱼ} (p : a == b) (q : b == c) (x : P a)
                     → ((transport P q) ∘ (transport P p)) x == transport P (p · q) x
    transport-comp-h {P = P} idp q x = idp {a =  (transport P q x)}

    -- A shorter notation for transport.
    _✶ : ∀ {ℓⱼ} {P : A → Type ℓⱼ} {a b : A} → a == b → P a → P b
    _✶ {ℓⱼ} {P} = transport {ℓᵢ = ℓᵢ} {ℓⱼ = ℓⱼ} P

  open Transport-Properties public

  ap-id : ∀{ℓᵢ} {A : Type ℓᵢ} {a b : A} (p : a == b) → ap id p == p
  ap-id idp = idp

  ap-comp : ∀{ℓᵢ ℓⱼ ℓₖ} {A : Type ℓᵢ} {B : Type ℓⱼ} {C : Type ℓₖ}  {a b : A}
          → (f : A → B) → (g : B → C) → (p : a == b)
          → ap g (ap f p) == ap (g ∘ f) p
  ap-comp f g idp = idp

  ap-const : ∀{ℓᵢ ℓⱼ} {A : Type ℓᵢ} {C : Type ℓⱼ} {a b : A} {c : C} (p : a == b)
           → ap (λ _ → c) p == idp
  ap-const {c = c} idp = idp {a = idp {a = c}}

  ap-· : ∀{ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} {a b c : A}
       → (f : A → B) → (p : a == b) → (q : b == c)
       → ap f (p · q) == ap f p · ap f q
  ap-· f idp q = idp {a = (ap f q)}

  ap-inv : ∀{ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} {a b : A}
         → (f : A → B) → (p : a == b)
         → ap f (inv p) == inv (ap f p)
  ap-inv f idp = idp

  transport-eq-fun-l : ∀{ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} {b : B} (f : A → B) {x y : A}
                       → (p : x == y) (q : f x == b)
                       → transport (λ z → f z == b) p q == inv (ap f p) · q
  transport-eq-fun-l {b = b} f p q =
    begin
      transport (λ z → f z == b) p q      ==⟨ transport-eq-fun f (λ _ → b) p q ⟩
      inv (ap f p) · q · ap (λ _ → b) p   ==⟨ ap (inv (ap f p) · q ·_) (ap-const p) ⟩
      inv (ap f p) · q · idp           ==⟨ inv (·-runit _) ⟩
      inv (ap f p) · q
    ∎

  transport-eq-fun-r : ∀{ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} {b : B} (g : A → B) {x y : A}
                       → (p : x == y) (q : b == g x)
                       → transport (λ z → b == g z) p q == q · (ap g p)
  transport-eq-fun-r {b = b} g p q =
    begin
      transport (λ z → b == g z) p q      ==⟨ transport-eq-fun (λ _ → b) g p q ⟩
      inv (ap (λ _ → b) p) · q · ap g p   ==⟨ ·-assoc (inv (ap (λ _ → b) p)) q (ap g p) ⟩
      inv (ap (λ _ → b) p) · (q · ap g p) ==⟨ ap (λ u → inv u · (q · ap g p)) (ap-const p) ⟩
      (q · ap g p)
    ∎

  transport-inv-l : ∀{ℓ} {A B : Type ℓ} → (p : A == B) → (b : B)
                → transport (λ v → v) p (transport (λ v → v) (inv p) b) == b
  transport-inv-l idp b = idp

  transport-inv-r : ∀{ℓ} {A B : Type ℓ} → (p : A == B) → (a : A)
                → transport (λ v → v) (inv p) (transport (λ v → v) p a) == a
  transport-inv-r idp b = idp

  transport-family : ∀{ℓᵢ ℓⱼ ℓₖ} {A : Type ℓᵢ} {B : Type ℓⱼ} {P : B → Type ℓₖ}
                   → {f : A → B} → {x y : A} → (p : x == y) → (u : P (f x))
                   → transport (P ∘ f) p u == transport P (ap f p) u
  transport-family idp u = idp

  transport-family-id : ∀{ℓᵢ ℓₖ} {A : Type ℓᵢ} {P : A → Type ℓₖ}
                   → {x y : A} → (p : x == y) → (u : P x)
                   → transport (λ a → P a) p u == transport P p u
  transport-family-id idp u = idp

  transport-fun : ∀{ℓᵢ ℓⱼ ℓₖ} {X : Type ℓᵢ} {x y : X} {A : X → Type ℓⱼ} {B : X → Type ℓₖ}
                  → (p : x == y) → (f : A x → B x)
                  → transport (λ x → (A x → B x)) p f == (λ x → transport B p (f (transport A (inv p) x)))
  transport-fun idp f = idp

  apd : ∀{ℓᵢ ℓⱼ} {A : Type ℓᵢ}  {P : A → Type ℓⱼ} {a b : A}
      → (f : (a : A) → P a) → (p : a == b)
      → transport P p (f a) == f b
  apd f idp = idp


  module Homotopy {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {P : A → Type ℓⱼ} where
    -- A homotopy is a natural isomorphism between two functions, we will write
    -- f ∼ g when (f x == g x) for all x.
    homotopy : (f g : ((x : A) → P x)) → Type (ℓᵢ ⊔ ℓⱼ)
    homotopy f g = (x : A) → f x == g x

    _∼_ : (f g : ((x : A) → P x)) → Type (ℓᵢ ⊔ ℓⱼ)
    f ∼ g = homotopy f g

    -- Homotopy is an equivalence relation
    h-refl : (f : (x : A) → P x) → f ∼ f
    h-refl f x = idp

    h-simm : (f g : (x : A) → P x) → f ∼ g → g ∼ f
    h-simm f g u x = inv (u x)

    h-comp : (f g h : (x : A) → P x) → f ∼ g → g ∼ h → f ∼ h
    h-comp f g h u v x = (u x)·(v x)

    _●_ : {f g h : (x : A) → P x} → f ∼ g → g ∼ h → f ∼ h
    α ● β = h-comp _ _ _ α β

  open Homotopy public

  -- Composition with homotopies
  module HomotopyComposition {ℓᵢ ℓⱼ ℓₖ} {A : Type ℓᵢ} {B : Type ℓⱼ} {C : Type ℓₖ} where
    hl-comp : (f g : A → B) → (j k : B → C) → f ∼ g → j ∼ k → (j ∘ f) ∼ (k ∘ g)
    hl-comp f g j k α β x = ap j (α x) · β (g x)

    rcomp-∼ : (f : A → B) → {j k : B → C} → j ∼ k → (j ∘ f) ∼ (k ∘ f)
    rcomp-∼ f β = hl-comp _ _ _ _ (h-refl f) β

    lcomp-∼ : {f g : A → B} → (j : B → C) → f ∼ g → (j ∘ f) ∼ (j ∘ g)
    lcomp-∼ j α = hl-comp _ _ _ _ α (h-refl j)

  open HomotopyComposition public

  module Fibers {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ}  where

    -- The fiber of a map over a point is given by
    fib : (f : A → B) → B → Type (ℓᵢ ⊔ ℓⱼ)
    fib f b = Σ A (λ a → f a == b)

    -- A function applied over the fiber returns the original point
    fib-eq : {f : A → B} → {b : B} → (h : fib f b) → f (π₁ h) == b
    fib-eq (a , α) = α

    -- Each point is on the fiber of its image
    fib-image : {f : A → B} → {a : A} → fib f (f a)
    fib-image {f} {a} = a , idp

  open Fibers public

  module Contractible where

    -- Contractible types. A contractible type is a type such that every
    -- element is equal to a center of contraction.
    isContr : ∀{ℓ}  (A : Type ℓ) → Type ℓ
    isContr A = Σ A (λ a → ((x : A) → a == x))
  open Contractible public

  module Equivalence where

    module DefinitionOfEquivalence {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} where
      -- Contractible maps. A map is contractible if the fiber in any
      -- point is contractible, that is, each element has a unique
      -- preimage.
      isContrMap : (f : A → B) → Type (ℓᵢ ⊔ ℓⱼ)
      isContrMap f = (b : B) → isContr (fib f b)

      -- There exists an equivalence between two types if there exists a
      -- contractible function between them.
      isEquiv : (f : A → B) → Type (ℓᵢ ⊔ ℓⱼ)
      isEquiv = isContrMap
    open DefinitionOfEquivalence public

    -- Equivalence of types.
    _≃_ : ∀{ℓᵢ ℓⱼ}  (A : Type ℓᵢ) (B : Type ℓⱼ) → Type (ℓᵢ ⊔ ℓⱼ)
    A ≃ B = Σ (A → B) isEquiv

    module EquivalenceMaps {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} where

      -- Maps of an equivalence
      lemap : A ≃ B → (A → B)
      lemap = π₁
      fun≃ = lemap

      remap : A ≃ B → (B → A)
      remap (f , contrf) b = π₁ (π₁ (contrf b))

      -- The maps of an equivalence are inverses in particular
      lrmap-inverse : (eq : A ≃ B) → {b : B} → (lemap eq) ((remap eq) b) == b
      lrmap-inverse (f , eqf) {b} = fib-eq (π₁ (eqf b))

      rlmap-inverse : (eq : A ≃ B) → {a : A} → (remap eq) ((lemap eq) a) == a
      rlmap-inverse (f , eqf) {a} = ap π₁ ((π₂ (eqf (f a))) fib-image)

      lrmap-inverse-h : (eq : A ≃ B) → ((lemap eq) ∘ (remap eq)) ∼ id
      lrmap-inverse-h eq = λ x → lrmap-inverse eq {x}

      rlmap-inverse-h : (eq : A ≃ B) → ((remap eq) ∘ (lemap eq)) ∼ id
      rlmap-inverse-h eq = λ x → rlmap-inverse eq {x}
    open EquivalenceMaps public

  open Equivalence public

  module FunctionExtensionality {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : A → Type ℓⱼ} {f g : (a : A) → B a} where
    -- Application of an homotopy
    happly : f == g → ((x : A) → f x == g x)
    happly idp x = idp

    -- The axiom of function extensionality postulates that the
    -- application of homotopies is an equivalence.
    postulate axiomFunExt : isEquiv happly

    eqFunExt : (f == g) ≃ ((x : A) → f x == g x)
    eqFunExt = happly , axiomFunExt

    -- From this, the usual notion of function extensionality follows.
    funext : ((x : A) → f x == g x) → f == g
    funext = remap eqFunExt

    -- Beta and eta rules for function extensionality
    funext-β : (h : ((x : A) → f x == g x)) → happly (funext h) == h
    funext-β h = lrmap-inverse eqFunExt

    funext-η : (p : f == g) → funext (happly p) == p
    funext-η p = rlmap-inverse eqFunExt

  open FunctionExtensionality public

  -- Function extensionality in the transport case
  module FunctionExtensionalityTransport
    {ℓᵢ ℓⱼ} {X : Type ℓᵢ} {A B : X → Type ℓⱼ} {x y : X} where

    funext-transport
      : (p : x == y) → (f : A x → B x) → (g : A y → B y)
      → ((p ✶) f == g) ≃ ((a : A(x)) → (p ✶) (f a) == g ((p ✶) a))
    funext-transport idp f g = eqFunExt

    funext-transport-l
      : (p : x == y) → (f : A x → B x) → (g : A y → B y)
      → ((p ✶) f == g) → ((a : A(x)) → (p ✶) (f a) == g ((p ✶) a))
    funext-transport-l p f g = lemap (funext-transport p _ _)

    funext-transport-r
      : (p : x == y) → (f : A x → B x) → (g : A y → B y)
      → ((a : A(x)) → (p ✶) (f a) == g ((p ✶) a)) → ((p ✶) f == g)
    funext-transport-r p f g = remap (funext-transport p _ _)

  open FunctionExtensionalityTransport public

  module Sigma {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {P : A → Type ℓⱼ} where

    -- Two dependent pairs are equal if they are componentwise equal.
    Σ-componentwise : {v w : Σ A P} → v == w → Σ (π₁ v == π₁ w) (λ p → (p ✶) (π₂ v) == π₂ w)
    Σ-componentwise  idp = (idp , idp)

    Σ-bycomponents : {v w : Σ A P} → Σ (π₁ v == π₁ w) (λ p → (p ✶) (π₂ v) == π₂ w) → v == w
    Σ-bycomponents (idp , idp) = idp
    pair= = Σ-bycomponents

    uppt : (x : Σ A P) → (π₁ x , π₂ x) == x
    uppt (a , b) = idp

    Σ-ap-π₁ : {a₁ a₂ : A} {b₁ : P a₁} {b₂ : P a₂}
      → (α : a₁ == a₂) → (γ : transport P α b₁ == b₂)
      → ap π₁ (pair= (α , γ)) == α
    Σ-ap-π₁ idp idp = idp
    ap-π₁-pair= = Σ-ap-π₁

  open Sigma public

  module CartesianProduct {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} where

    -- In a pair, the equality of the two components of the pairs is
    -- equivalent to equality of the two pairs.
    prodComponentwise : {x y : A × B} → (x == y) → ((π₁ x == π₁ y) × (π₂ x == π₂ y))
    π₁ (prodComponentwise idp) = idp
    π₂ (prodComponentwise idp) = idp

    prodByComponents : {x y : A × B} → ((π₁ x == π₁ y) × (π₂ x == π₂ y)) → (x == y)
    prodByComponents (idp , idp) = idp

    -- This is in fact an equivalence.
    prodCompInverse : {x y : A × B} (b : ((π₁ x == π₁ y) × (π₂ x == π₂ y))) →
                      prodComponentwise (prodByComponents b) == b
    prodCompInverse (idp , idp) = idp

    prodByCompInverse : {x y : A × B} (b : x == y) →
                      prodByComponents (prodComponentwise b) == b
    prodByCompInverse idp = idp

  open CartesianProduct public

  module Propositions where

    -- A type is a mere proposition if any two inhabitants of the type
    -- are equal
    isProp : ∀{ℓ}  (A : Type ℓ) → Type ℓ
    isProp A = ((x y : A) → x == y)

    -- The type of mere propositions
    hProp : ∀{ℓ} → Type (lsuc ℓ)
    hProp {ℓ} = Σ (Type ℓ) isProp


    -- The dependent function type to proposition types is itself a
    -- proposition.
    piProp : ∀{ℓᵢ ℓⱼ} → {A : Type ℓᵢ} → {B : A → Type ℓⱼ}
           → ((a : A) → isProp (B a)) → isProp ((a : A) → B a)
    piProp props f g = funext λ a → props a (f a) (g a)

    -- The product of propositions is itself a proposition.
    isProp-prod : ∀{ℓᵢ ℓⱼ} → {A : Type ℓᵢ} → {B : Type ℓⱼ}
                → isProp A → isProp B → isProp (A × B)
    isProp-prod p q x y = prodByComponents ((p _ _) , (q _ _))

  open Propositions public

  module Sets where

    -- A type is a "set" by definition if any two equalities on the type
    -- are equal.
    isSet : ∀{ℓ}  (A : Type ℓ) → Type ℓ
    isSet A = (x y : A) → isProp (x == y)

    -- The type of sets.
    hSet : ∀{ℓ} → Type (lsuc ℓ)
    hSet {ℓ} = Σ (Type ℓ) isSet

    -- Product of sets is a set.
    isSet-prod : ∀{ℓᵢ ℓⱼ}  {A : Type ℓᵢ} → {B : Type ℓⱼ}
               → isSet A → isSet B → isSet (A × B)
    isSet-prod sa sb (a , b) (c , d) p q = begin
       p
        ==⟨ inv (prodByCompInverse p) ⟩
       prodByComponents (prodComponentwise p)
        ==⟨ ap prodByComponents (prodByComponents (sa a c _ _ , sb b d _ _)) ⟩
       prodByComponents (prodComponentwise q)
        ==⟨ prodByCompInverse q ⟩
       q
      ∎

  open Sets public

  module HLevels where

    -- Propositions are Sets.
    propIsSet : ∀{ℓ} {A : Type ℓ} → isProp A → isSet A
    propIsSet {A = A} f a _ p q = lemma p · inv (lemma q)
      where
        triang : {y z : A} {p : y == z} → (f a y) · p == f a z
        triang {b}{p = idp} = inv (·-runit (f a b))

        lemma : {y z : A} (p : y == z) → p == inv (f a y) · (f a z)
        lemma {y} {z} p =
          begin
            p                         ==⟨ ap (_· p) (inv (·-linv (f a y))) ⟩
            inv (f a y) · f a y · p   ==⟨ ·-assoc (inv (f a y)) (f a y) p ⟩
            inv (f a y) · (f a y · p) ==⟨ ap (inv (f a y) ·_) triang ⟩
            inv (f a y) · (f a z)
          ∎

    -- Contractible types are Propositions.
    contrIsProp : ∀{ℓ}  {A : Type ℓ} → isContr A → isProp A
    contrIsProp (a , p) x y = inv (p x) · p y

    -- To be contractible is itself a proposition.
    isContrIsProp : ∀{ℓ}  {A : Type ℓ} → isProp (isContr A)
    isContrIsProp {_} {A} (a , p) (b , q) = Σ-bycomponents (inv (q a) , piProp (AisSet b) _ q)
      where
        AisSet : isSet A
        AisSet = propIsSet (contrIsProp (a , p))

  open HLevels public

  module EquivalenceProp {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} where

    -- Contractible maps are propositions
    isContrMapIsProp : (f : A → B) → isProp (isContrMap f)
    isContrMapIsProp f = piProp λ a → isContrIsProp

    isEquivIsProp : (f : A → B) → isProp (isEquiv f)
    isEquivIsProp = isContrMapIsProp

    -- Equality of same-morphism equivalences
    sameEqv : {α β : A ≃ B} → π₁ α == π₁ β → α == β
    sameEqv {(f , σ)} {(g , τ)} p = Σ-bycomponents (p , (isEquivIsProp g _ τ))

    -- Equivalences preserve propositions
    isProp-≃ : (A ≃ B) → isProp A → isProp B
    isProp-≃ eq prop x y =
      begin
        x                       ==⟨ inv (lrmap-inverse eq) ⟩
        lemap eq ((remap eq) x) ==⟨ ap (λ u → lemap eq u) (prop _ _) ⟩
        lemap eq ((remap eq) y) ==⟨ lrmap-inverse eq ⟩
        y
      ∎

  open EquivalenceProp public

  module Naturality {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} where
    h-naturality : {f g : A → B} (H : f ∼ g) → {x y : A} → (p : x == y)
                 → H x · ap g p == ap f p · H y
    h-naturality  H {x = x} (idp ) = inv (·-runit (H x))
  open Naturality

  h-naturality-id : ∀{ℓ} {A : Type ℓ} {f : A → A} (H : f ∼ id) → {x : A}
                  → H (f x) == ap f (H x)
  h-naturality-id {f = f} H {x = x} =
    begin
      H (f x)                            ==⟨ ·-runit (H (f x)) ⟩
      H (f x) · (idp {a = f x})          ==⟨ ap (H (f x) ·_) (inv (·-rinv (H x))) ⟩
      H (f x) · (H x · inv (H x))        ==⟨ inv (·-assoc (H (f x)) _ (inv (H x))) ⟩
      H (f x) · H x · inv (H x)          ==⟨ ap (λ u → H (f x) · u · inv (H x)) (inv (ap-id _)) ⟩
      H (f x) · ap id (H x) · inv (H x)  ==⟨ ap (_· inv (H x)) (h-naturality H (H x)) ⟩
      ap f (H x) · H x · inv (H x)       ==⟨ ·-assoc (ap f (H x)) _ (inv (H x)) ⟩
      ap f (H x) · (H x · inv (H x))     ==⟨ ap (ap f (H x) ·_) (·-rinv (H x)) ⟩
      ap f (H x) · (idp {a = f x})       ==⟨ inv (·-runit (ap f (H x))) ⟩
      ap f (H x)
    ∎

  module Halfadjoints {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} where

    -- Half adjoint equivalence.
    record ishae (f : A → B) : Type (ℓᵢ ⊔ ℓⱼ) where
      constructor hae
      field
        g : B → A
        η : (g ∘ f) ∼ id
        ε : (f ∘ g) ∼ id
        τ : (a : A) → ap f (η a) == ε (f a)

    -- Half adjoint equivalences give contractible fibers.
    ishae-contr : (f : A → B) → ishae f → isContrMap f
    ishae-contr f (hae g η ε τ) y = ((g y) , (ε y)) , contra
      where
        lemma : (c c' : fib f y) → Σ (π₁ c == π₁ c') (λ γ → (ap f γ) · π₂ c' == π₂ c) → c == c'
        lemma c c' (p , q) = Σ-bycomponents (p , lemma2)
          where
            lemma2 : transport (λ z → f z == y) p (π₂ c) == π₂ c'
            lemma2 =
              begin
                transport (λ z → f z == y) p (π₂ c)
                  ==⟨ transport-eq-fun-l f p (π₂ c) ⟩
                inv (ap f p) · (π₂ c)
                  ==⟨ ap (inv (ap f p) ·_) (inv q) ⟩
                inv (ap f p) · ((ap f p) · (π₂ c'))
                  ==⟨ inv (·-assoc (inv (ap f p)) (ap f p) (π₂ c')) ⟩
                inv (ap f p) · (ap f p) · (π₂ c')
                  ==⟨ ap (_· (π₂ c')) (·-linv (ap f p)) ⟩
                π₂ c'
              ∎

        contra : (x : fib f y) → (g y , ε y) == x
        contra (x , p) = lemma (g y , ε y) (x , p) (γ , lemma3)
          where
            γ : g y == x
            γ = inv (ap g p) · η x

            lemma3 : (ap f γ · p) == ε y
            lemma3 =
              begin
                ap f γ · p
                  ==⟨ ap (_· p) (ap-· f (inv (ap g p)) (η x)) ⟩
                ap f (inv (ap g p)) · ap f (η x) · p
                  ==⟨ ·-assoc (ap f (inv (ap g p))) _ p ⟩
                ap f (inv (ap g p)) · (ap f (η x) · p)
                  ==⟨ ap (_· (ap f (η x) · p)) (ap-inv f (ap g p)) ⟩
                inv (ap f (ap g p)) · (ap f (η x) · p)
                  ==⟨ ap (λ u → inv (ap f (ap g p)) · (u · p)) (τ x) ⟩
                inv (ap f (ap g p)) · (ε (f x) · p)
                  ==⟨ ap (λ u → inv (ap f (ap g p)) · (ε (f x) · u)) (inv (ap-id p)) ⟩
                inv (ap f (ap g p)) · (ε (f x) · ap id p)
                  ==⟨ ap (inv (ap f (ap g p)) ·_) (h-naturality ε p) ⟩
                inv (ap f (ap g p)) · (ap (f ∘ g) p · ε y)
                  ==⟨ ap (λ u → inv u · (ap (f ∘ g) p · ε y)) (ap-comp g f p) ⟩
                inv (ap (f ∘ g) p) · (ap (f ∘ g) p · ε y)
                  ==⟨ inv (·-assoc (inv (ap (f ∘ g) p)) _ (ε y)) ⟩
                (inv (ap (f ∘ g) p) · ap (f ∘ g) p) · ε y
                  ==⟨ ap (_· ε y) (·-linv (ap (λ z → f (g z)) p)) ⟩
                ε y
              ∎

    -- Half-adjointness implies equivalence.
    ishae-≃ : {f : A → B} → ishae f → A ≃ B
    ishae-≃ ishaef = _ , (ishae-contr _ ishaef)

  open Halfadjoints public

  module Quasiinverses {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {B : Type ℓⱼ} where

    -- Definitions for quasi-inverses, left-inverses, right-inverses and
    -- biinverses.
    qinv : (A → B) → Type (ℓᵢ ⊔ ℓⱼ)
    qinv f = Σ (B → A) (λ g → ((f ∘ g) ∼ id) × ((g ∘ f) ∼ id))

    linv : (A → B) → Type (ℓᵢ ⊔ ℓⱼ)
    linv f = Σ (B → A) (λ g → (g ∘ f) ∼ id)

    rinv : (A → B) → Type (ℓᵢ ⊔ ℓⱼ)
    rinv f = Σ (B → A) λ g → (f ∘ g) ∼ id

    biinv : (A → B) → Type (ℓᵢ ⊔ ℓⱼ)
    biinv f = linv f × rinv f

    qinv-biinv : (f : A → B) → qinv f → biinv f
    qinv-biinv f (g , (u1 , u2)) = (g , u2) , (g , u1)

    biinv-qinv : (f : A → B) → biinv f → qinv f
    biinv-qinv f ((h , α) , (g , β)) = g , (β , δ)
      where
        γ1 : g ∼ ((h ∘ f) ∘ g)
        γ1 = rcomp-∼ g (h-simm (h ∘ f) id α)

        γ2 : ((h ∘ f) ∘ g) ∼ (h ∘ (f ∘ g))
        γ2 x = idp

        γ : g ∼ h
        γ = γ1 ● (γ2 ● (lcomp-∼ h β))

        δ : (g ∘ f) ∼ id
        δ = (rcomp-∼ f γ) ● α

    equiv-biinv : (f : A → B) → isContrMap f → biinv f
    equiv-biinv f contrf =
      (remap eq , rlmap-inverse-h eq) , (remap eq , lrmap-inverse-h eq)
      where
        eq : A ≃ B
        eq = f , contrf

    -- Quasiinverses are halfadjoint equivalences.
    qinv-ishae : {f : A → B} → qinv f → ishae f
    qinv-ishae {f} (g , (ε , η)) = record {
        g = g ;
        η = η ;
        ε = λ b → inv (ε (f (g b))) · ap f (η (g b)) · ε b ;
        τ = τ
      }
      where
        lemma1 : (a : A) → ap f (η (g (f a))) · ε (f a) == ε (f (g (f a))) · ap f (η a)
        lemma1 a =
          begin
            ap f (η ((g ∘ f) a)) · ε (f a)
              ==⟨ ap (λ u → ap f u · ε (f a)) (h-naturality-id η) ⟩
            ap f (ap (g ∘ f) (η a)) · ε (f a)
              ==⟨ ap (_· ε (f a)) (ap-comp (g ∘ f) f (η a)) ⟩
            ap (f ∘ (g ∘ f)) (η a) · ε (f a)
              ==⟨ inv (h-naturality (λ x → ε (f x)) (η a)) ⟩
            ε (f (g (f a))) · ap f (η a)
          ∎

        τ : (a : A) → ap f (η a) == (inv (ε (f (g (f a)))) · ap f (η (g (f a))) · ε (f a))
        τ a =
          begin
            ap f (η a)
              ==⟨ ap (_· ap f (η a)) (inv (·-linv (ε (f (g (f a)))))) ⟩
            inv (ε (f (g (f a)))) · ε (f (g (f a))) · ap f (η a)
              ==⟨ ·-assoc (inv (ε (f (g (f a))))) _ (ap f (η a)) ⟩
            inv (ε (f (g (f a)))) · (ε (f (g (f a))) · ap f (η a))
              ==⟨ ap (inv (ε (f (g (f a)))) ·_) (inv (lemma1 a)) ⟩
            inv (ε (f (g (f a)))) · (ap f (η (g (f a))) · ε (f a))
              ==⟨ inv (·-assoc (inv (ε (f (g (f a))))) _ (ε (f a))) ⟩
            inv (ε (f (g (f a)))) · ap f (η (g (f a))) · ε (f a)
          ∎

    -- Quasiinverses create equivalences.
    qinv-≃ : (f : A → B) → qinv f → A ≃ B
    qinv-≃ f = ishae-≃ ∘ qinv-ishae

    ≃-qinv : A ≃ B → Σ (A → B) qinv
    ≃-qinv eq =
      lemap eq , (remap eq , (lrmap-inverse-h eq , rlmap-inverse-h eq))

    -- Half-adjoint equivalences are quasiinverses.
    ishae-qinv : {f : A → B} → ishae f → qinv f
    ishae-qinv {f} (hae g η ε τ) = g , (ε , η)

    ≃-ishae : (e : A ≃ B)→ ishae (lemap e)
    ≃-ishae e = qinv-ishae (π₂ (≃-qinv e))

  open Quasiinverses public

  module EquivalenceComposition where

    -- Composition of quasiinverses
    qinv-comp : ∀{ℓ} {A B C : Type ℓ} → Σ (A → B) qinv → Σ (B → C) qinv → Σ (A → C) qinv
    qinv-comp (f , (if , (εf , ηf))) (g , (ig , (εg , ηg))) = (g ∘ f) , ((if ∘ ig) ,
       ( (λ x → ap g (εf (ig x)) · εg x)
       ,  λ x → ap if (ηg (f x)) · ηf x))

    qinv-inv : ∀{ℓ} {A B : Type ℓ} → Σ (A → B) qinv → Σ (B → A) qinv
    qinv-inv (f , (g , (ε , η))) = g , (f , (η , ε))

    -- Composition of equivalences
    idEqv : ∀{ℓ} {A : Type ℓ} → A ≃ A
    idEqv = id , λ a → (a , idp) , λ { (_ , idp) → idp }

    compEqv : ∀{ℓ} {A B C : Type ℓ} → A ≃ B → B ≃ C → A ≃ C
    compEqv {ℓ} {A} {B} {C} eqf eqg = qinv-≃ (π₁ qcomp) (π₂ qcomp)
     where
       qcomp : Σ (A → C) qinv
       qcomp = qinv-comp (≃-qinv eqf) (≃-qinv eqg)

    invEqv : ∀{ℓ} {A B : Type ℓ} → A ≃ B → B ≃ A
    invEqv {ℓ} {A} {B} eqf = qinv-≃ (π₁ qcinv) (π₂ qcinv)
     where
       qcinv : Σ (B → A) qinv
       qcinv = qinv-inv (≃-qinv eqf)

    -- Lemmas about composition
    compEqv-inv : ∀{ℓ} {A B : Type ℓ} → (α : A ≃ B) → compEqv α (invEqv α) == idEqv
    compEqv-inv {_} {A} {B} α = sameEqv (
     begin
       π₁ (compEqv α (invEqv α)) ==⟨ idp ⟩
       π₁ (invEqv α) ∘ π₁ α     ==⟨ funext (rlmap-inverse-h α) ⟩
       id
     ∎)

  open EquivalenceComposition public


  module SigmaEquivalence {ℓᵢ ℓⱼ} {A : Type ℓᵢ} {P : A → Type ℓⱼ} where

    pair=Equiv : {v w : Σ A P}
      → Σ (π₁ v == π₁ w) (λ p → (p ✶) (π₂ v) == π₂ w) ≃ v == w
    pair=Equiv = qinv-≃ Σ-bycomponents (Σ-componentwise , HΣ₁ , HΣ₂)
      where
        HΣ₁ : Σ-bycomponents ∘ Σ-componentwise ∼ id
        HΣ₁ idp = idp

        HΣ₂ : Σ-componentwise ∘ Σ-bycomponents ∼ id
        HΣ₂ (idp , idp) = idp

    private
      f : {a₁ a₂ : A} {α : a₁ == a₂}{c₁ : P a₁} {c₂ : P a₂}
        → {β : a₁ == a₂}
        → {γ : transport P β c₁ == c₂}
        → ap π₁ (pair= (β , γ)) == α → β == α
      f {β = idp} {γ = idp} idp = idp

      g : {a₁ a₂ : A} {α : a₁ == a₂}{c₁ : P a₁} {c₂ : P a₂}
        → {β : a₁ == a₂}
        → {γ : transport P β c₁ == c₂}
        → β == α → ap π₁ (pair= (β , γ)) == α
      g {β = idp} {γ = idp} idp = idp

      f-g : {a₁ a₂ : A} {α : a₁ == a₂}{c₁ : P a₁} {c₂ : P a₂}
        → {β : a₁ == a₂}
        → {γ : transport P β c₁ == c₂}
        → f {α = α}{β = β}{γ} ∘ g {α = α}{β = β} ∼ id
      f-g {β = idp} {γ = idp} idp = idp

      g-f : {a₁ a₂ : A} {α : a₁ == a₂}{c₁ : P a₁} {c₂ : P a₂}
        → {β : a₁ == a₂}
        → {γ : transport P β c₁ == c₂}
        → g {α = α}{β = β}{γ} ∘ f {α = α}{β = β}{γ} ∼ id
      g-f {β = idp} {γ = idp} idp = idp

    ap-π₁-pair=Equiv : {a₁ a₂ : A} {c₁ : P a₁} {c₂ : P a₂}
      → (α : a₁ == a₂)
      → (γ : Σ (a₁ == a₂) (λ α' → transport P α' c₁ == c₂))
      → (ap π₁ (pair= γ) == α) ≃ π₁ γ == α
    ap-π₁-pair=Equiv {a₁ = a₁} α (β , γ) = qinv-≃ f (g , f-g , g-f)

  open SigmaEquivalence public

  -- Univalence Axiom definition.

  module Univalence where

    -- Voevodsky's Univalence Axiom.
    module UnivalenceAxiom {ℓ} {A B : Type ℓ} where

      idtoeqv : A == B → A ≃ B
      idtoeqv p = qinv-≃
        (transport (λ x → x) p)
        (transport (λ x → x) (inv p) , (transport-inv-l p , transport-inv-r p))

      -- The Univalence axiom induces an equivalence between equalities
      -- and equivalences.
      postulate axiomUnivalence : isEquiv idtoeqv
      eqvUnivalence : (A == B) ≃ (A ≃ B)
      eqvUnivalence = idtoeqv , axiomUnivalence

      -- Introduction rule for equalities.
      ua : A ≃ B → A == B
      ua = remap eqvUnivalence

      -- Computation rules
      ua-β : (eqv : A ≃ B) → idtoeqv (ua eqv) == eqv
      ua-β eqv = lrmap-inverse eqvUnivalence

      ua-η : (p : A == B) → ua (idtoeqv p) == p
      ua-η p = rlmap-inverse eqvUnivalence
    open UnivalenceAxiom public
  open Univalence public

  module EquivalenceReasoning where

    infixr 2 _≃⟨⟩_
    _≃⟨⟩_ : ∀ {ℓ} (A {B} : Type ℓ) → A ≃ B → A ≃ B
    _ ≃⟨⟩ e = e

    infixr 2 _≃⟨_⟩_
    _≃⟨_⟩_ : ∀ {ℓ} (A : Type ℓ) {B C : Type ℓ} → A ≃ B → B ≃ C → A ≃ C
    _ ≃⟨ e₁ ⟩ e₂ = compEqv e₁ e₂
    --
    infix  3 _≃∎
    _≃∎ :  ∀ {ℓ} (A : Type ℓ) → A ≃ A
    _≃∎ = λ A → idEqv {A = A}

    infix  1 begin≃_
    begin≃_ : ∀ {ℓ} {A B : Type ℓ} → A ≃ B → A ≃ B
    begin≃_ e = e

  open EquivalenceReasoning public

  module TransportUA where

    transport-family-ap
      : ∀ {ℓ} {A : Type ℓ}
      → (B : A → Type ℓ)
      → {x y : A}
      → (p : x == y)
      → (u : B x)
      ---------------------------------------------------
      → transport B p u == transport (λ X → X) (ap B p) u
    transport-family-ap B idp u = idp

    transport-family-idtoeqv
      : ∀ {ℓ} {A : Type ℓ}
      → (B : A → Type ℓ)
      → {x y : A}
      → (p : x == y)
      → (u : B x)
      ---------------------------------------------------
      → transport B p u == fun≃ (idtoeqv (ap B p)) u
    transport-family-idtoeqv B idp u = idp

    transport-ua
      : ∀ {ℓ} {A : Type ℓ}
      → (B : A → Type ℓ)
      → {x y : A}
      → (p : x == y)
      → (e : B x ≃ B y)
      → ap B p == ua e
      -----------------
      → (u : B x) → transport B p u == (fun≃ e) u
    transport-ua B idp e q u =
      begin
        transport B idp u
          ==⟨ transport-family-idtoeqv B idp u ⟩
        fun≃ (idtoeqv (ap B idp)) u
          ==⟨ ap (λ r → fun≃ (idtoeqv r) u) q ⟩
        fun≃ (idtoeqv (ua e)) u
          ==⟨ ap (λ r → fun≃ r u) (ua-β e) ⟩
        fun≃ e u
      ∎

  open TransportUA public

open hott public

Let be α : A == B, a : A, and b : B then the following types are equivalent to the previous type HEq₁.

HEq₂ : ∀ {ℓ} (A : Type ℓ)(B : Type ℓ) (α : A == B)(a : A)(b : B) → Type ℓ
HEq₂ A B α a b = Path (coe α a) b

HEq₃ : ∀ {ℓ} (A : Type ℓ)(B : Type ℓ) (α : A == B)(a : A)(b : B) → Type ℓ
HEq₃ A B α a b = Path a (coe (inv α) b)

HEq₄ : ∀ {ℓ} (A : Type ℓ)(B : Type ℓ) (α : A == B)(a : A)(b : B) → Type ℓ
HEq₄ A .A idp a b = Path a b

Equivalences

The following equivalences are all provable by path-induction, we do path induction on the path α from the definition above and depending on the heterogeneous equality definition we chose we might be need other path induction. The convention for the equivalences is HEqᵢ-≃-HEqⱼ to denote the evidence of the equivalence between the type HEqᵢ and HEqⱼ.

Let us prove the equivalence between the types HEq₁ and HEq₂. The other equivalences are proved in a similar way and they are available on the website that supports this document.

-- HEq₁-≃-HEq₂
module _ {ℓ}(A : Type ℓ) (B : Type ℓ) where

-- Outgoing functions
  HEq₁-to-HEq₂
    : {α : A == B}{a : A}{b : B}
    → HEq₁ A B α a b
    → HEq₂ A B α a b

  HEq₁-to-HEq₂ {idp} idp = idp

  HEq₂-to-HEq₁
    : {α : A == B}{a : A}{b : B}
    → HEq₂ A B α a b
    → HEq₁ A B α a b

  HEq₂-to-HEq₁ {idp} idp = idp

Finally, we provide the evidence of the equivalence.

-- Equivalence
  HEq₁-≃-HEq₂
    : {α : A == B}{a : A}{b : B}
    → HEq₁ A B α a b ≃ HEq₂ A B α a b

  HEq₁-≃-HEq₂ {idp} {a} {b} =
    qinv-≃ HEq₁-to-HEq₂ (HEq₂-to-HEq₁ , HEq₁-~-HEq₂ , HEq₂-~-HEq₁)
    where
      HEq₁-~-HEq₂ : ( p : HEq₂ A B idp a b)
                  → ( HEq₁-to-HEq₂ (HEq₂-to-HEq₁ p ) == p)
      HEq₁-~-HEq₂ idp = idp

      HEq₂-~-HEq₁ : ( p : HEq₁ A B idp a b)
                  → ( HEq₂-to-HEq₁ (HEq₁-to-HEq₂ p ) == p)
      HEq₂-~-HEq₁ idp = idp

-- Other equivalences:  HEq₂-≃-HEq₃, HEq₃-≃-HEq₄, HEq₄-≃-HEq₁

-- HEq₂-≃-HEq₃

module _ {ℓ}(A : Type ℓ) (B : Type ℓ) where

  HEq₂-to-HEq₃ : {α : A == B}{a : A}{b : B}
               → HEq₂ A B α a b
               → HEq₃ A B α a b
  HEq₂-to-HEq₃ {idp}  idp = idp

  HEq₃-to-HEq₂ : {α : A == B}{a : A}{b : B}
               → HEq₃ A B α a b
               → HEq₂ A B α a b
  HEq₃-to-HEq₂ {idp} idp = idp

  HEq₂-≃-HEq₃ : {α : A == B}{a : A}{b : B}
             → HEq₂ A B α a b ≃ HEq₃ A B α a b
  HEq₂-≃-HEq₃ {idp} {a} {b} =
    qinv-≃ HEq₂-to-HEq₃ (HEq₃-to-HEq₂ , HEq₂-~-HEq₃ , HEq₃-~-HEq₂)
    where
      HEq₂-~-HEq₃ : ( p : HEq₃ A B idp a b)
                  → ( HEq₂-to-HEq₃ (HEq₃-to-HEq₂ p ) == p)
      HEq₂-~-HEq₃ idp = idp

      HEq₃-~-HEq₂ : ( p : HEq₂ A B idp a b)
                  → ( HEq₃-to-HEq₂ (HEq₂-to-HEq₃ p ) == p)
      HEq₃-~-HEq₂ idp = idp

-- HEq₃-≃-HEq₄

module _ {ℓ}(A : Type ℓ) (B : Type ℓ) where

  HEq₃-to-HEq₄ : {α : A == B}{a : A}{b : B}
               → HEq₃ A B α a b
               → HEq₄ A B α a b
  HEq₃-to-HEq₄ {idp}  idp = idp

  HEq₄-to-HEq₃ : {α : A == B}{a : A}{b : B}
               → HEq₄ A B α a b
               → HEq₃ A B α a b
  HEq₄-to-HEq₃ {idp} idp = idp

  HEq₃-≃-HEq₄ : {α : A == B}{a : A}{b : B}
             → HEq₃ A B α a b ≃ HEq₄ A B α a b
  HEq₃-≃-HEq₄ {idp} {a} {b} =
    qinv-≃ HEq₃-to-HEq₄ (HEq₄-to-HEq₃ , HEq₃-~-HEq₄ , HEq₄-~-HEq₃)
    where
      HEq₃-~-HEq₄ : ( p : HEq₄ A B idp a b)
                  → ( HEq₃-to-HEq₄ (HEq₄-to-HEq₃ p ) == p)
      HEq₃-~-HEq₄ idp = idp

      HEq₄-~-HEq₃ : ( p : HEq₃ A B idp a b)
                  → ( HEq₄-to-HEq₃ (HEq₃-to-HEq₄ p ) == p)
      HEq₄-~-HEq₃ idp = idp

-- HEq₄-≃-HEq₁

module _ {ℓ}(A : Type ℓ) (B : Type ℓ) where

  HEq₄-to-HEq₁ : {α : A == B}{a : A}{b : B}
               → HEq₄ A B α a b
               → HEq₁ A B α a b
  HEq₄-to-HEq₁ {idp} idp = idp

  HEq₁-to-HEq₄ : {α : A == B}{a : A}{b : B}
               → HEq₁ A B α a b
               → HEq₄ A B α a b
  HEq₁-to-HEq₄ {idp} idp = idp

  HEq₄-≃-HEq₁ : {α : A == B}{a : A}{b : B}
             → HEq₄ A B α a b ≃ HEq₁ A B α a b
  HEq₄-≃-HEq₁ {idp} {a} {b} =
    qinv-≃ HEq₄-to-HEq₁ (HEq₁-to-HEq₄ , HEq₄-~-HEq₁ , HEq₁-~-HEq₄)
    where
      HEq₄-~-HEq₁ : ( p : HEq₁ A B idp a b)
                  → ( HEq₄-to-HEq₁ (HEq₁-to-HEq₄ p ) == p)
      HEq₄-~-HEq₁ idp = idp

      HEq₁-~-HEq₄ : ( p : HEq₄ A B idp a b)
                  → ( HEq₁-to-HEq₄ (HEq₄-to-HEq₁ p ) == p)
      HEq₁-~-HEq₄ idp = idp

We prefer to use definition HEq₁ as the definition by default for heterogeneous equality. We later on refer to this type as HEq.

HEq = HEq₂

Paths in the total space

As we mentioned above, Pathover can be defined in at least five different ways. An inductive definition, using the heterogeneous equality, transporting along homogeneous equalities and the last one by path-induction on the identity type.

data PathOver₁ {ℓᵢ ℓⱼ} {A : Set ℓᵢ} (C : A → Type ℓⱼ) {a₁ : A}
  : {a₂ : A} (α : a₁ == a₂) (c₁ : C a₁) (c₂ : C a₂) → Type (ℓᵢ ⊔ ℓⱼ) where
  idp : ∀ {c₁ : C a₁} → PathOver₁ C idp c₁ c₁

PathOver₂
  : ∀ {ℓᵢ ℓⱼ} {A : Type ℓᵢ}
  → (C : A → Type ℓⱼ) {a₁ a₂ : A}
  → (α : a₁ == a₂)
  → (c₁ : C a₁)
  → (c₂ : C a₂)
  -------------------
  → Type ℓⱼ

PathOver₂ {A = A} C {a₁} {a₂} α c₁ c₂ = HEq (C a₁) (C a₂) (ap C α) c₁ c₂

PathOver₃
  : ∀ {ℓᵢ ℓⱼ} {A : Type ℓᵢ}
  → (C : A → Type ℓⱼ) {a₁ a₂ : A}
  → (α : a₁ == a₂)
  → (c₁ : C a₁)
  → (c₂ : C a₂)
  -------------------
  → Type ℓⱼ

PathOver₃ C α c₁ c₂ = transport C α c₁ == c₂

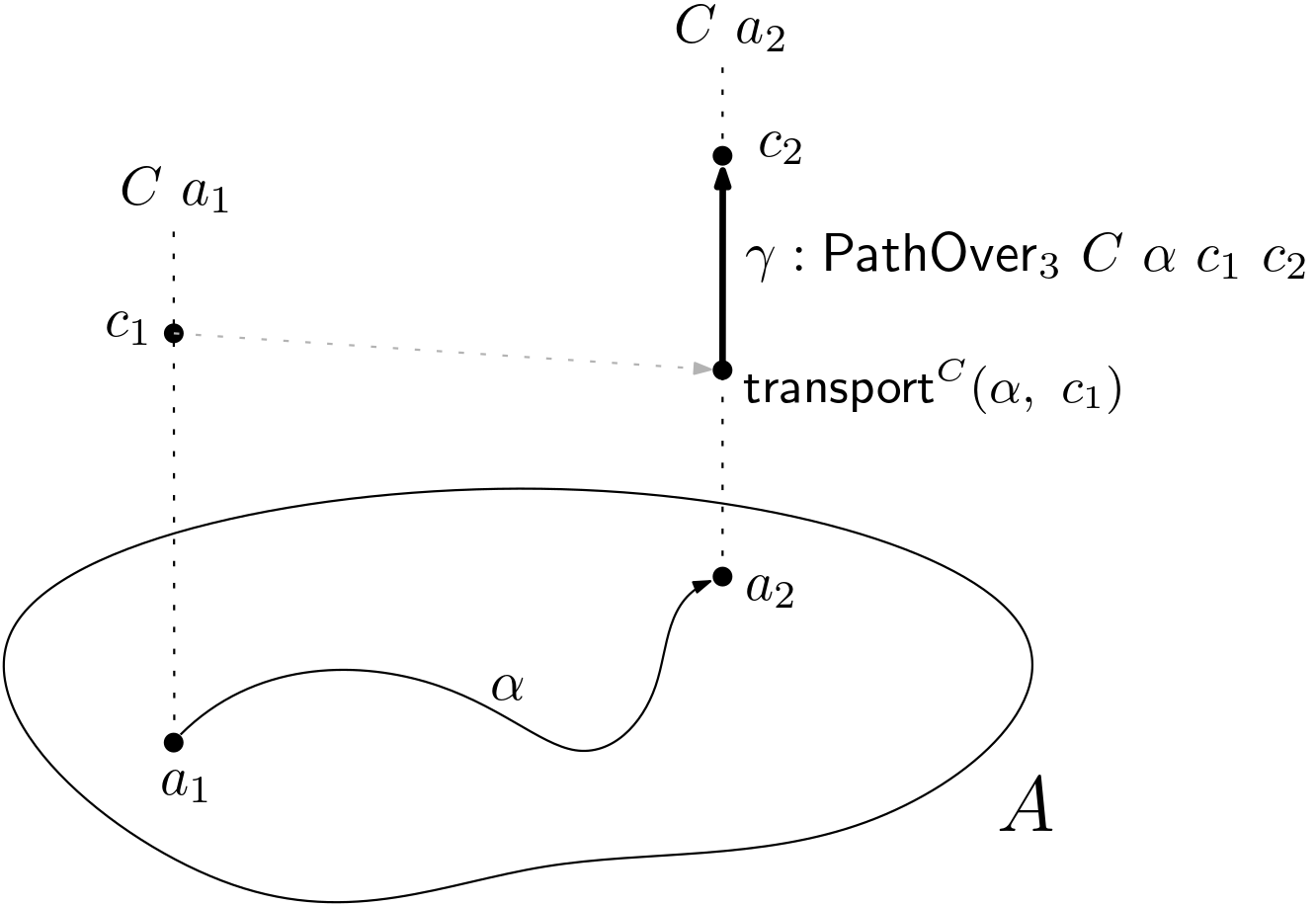Figure 2. Pathover₃.

PathOver₄
  : ∀ {ℓᵢ ℓⱼ} {A : Type ℓᵢ}
  → (C : A → Type ℓⱼ) {a₁ a₂ : A}
  → (α : a₁ == a₂)
  → (c₁ : C a₁)
  → (c₂ : C a₂)
  -------------------
  → Type ℓⱼ

PathOver₄ C α c₁ c₂ = c₁ == transport C (α ⁻¹) c₂

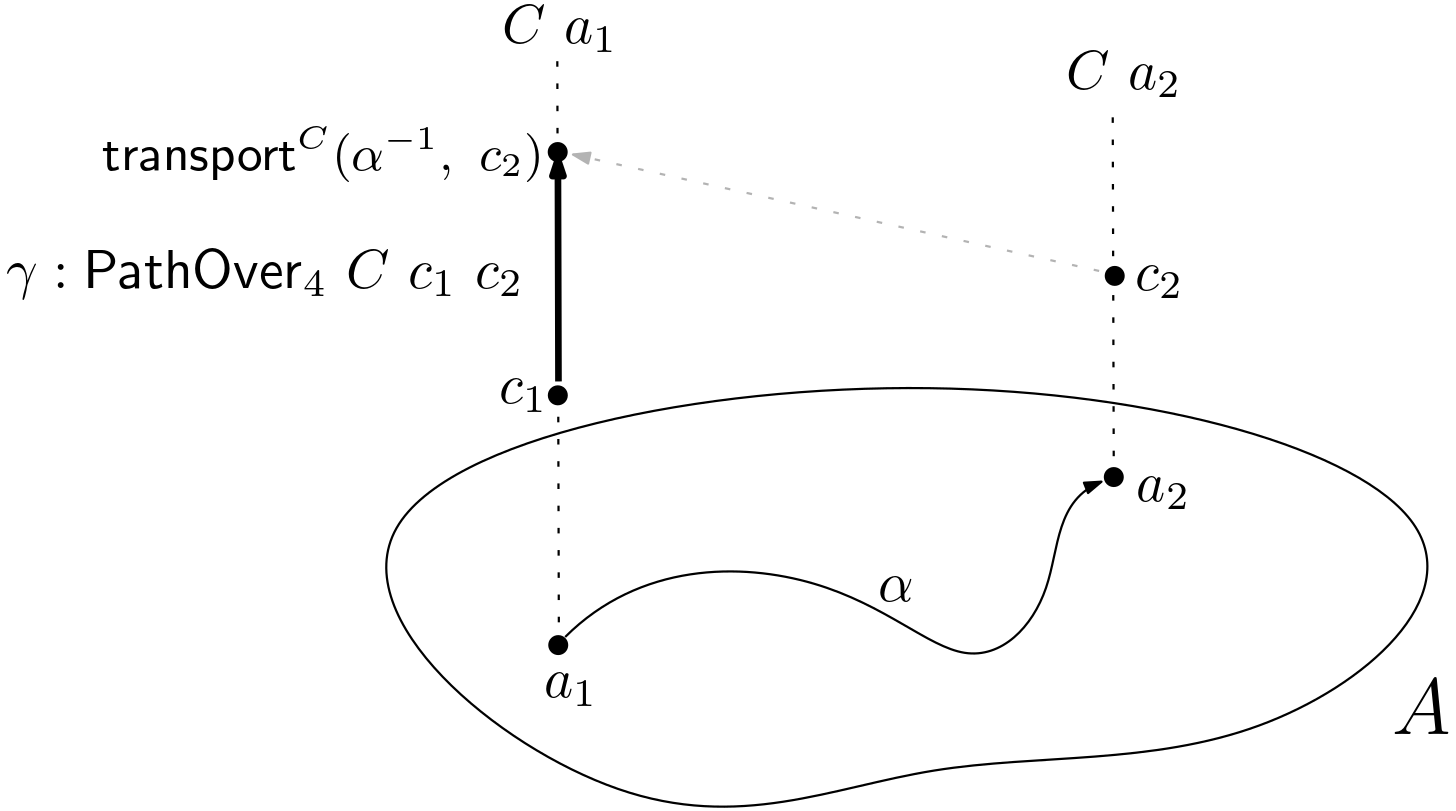Figure 3. Pathover₄.

PathOver₅
  : ∀ {ℓᵢ ℓⱼ} {A : Type ℓᵢ}
  → (C : A → Type ℓⱼ) {a₁ a₂ : A}
  → (α : a₁ == a₂)
  → (c₁ : C a₁)
  → (c₂ : C a₂)
  -------------------
  → Type ℓⱼ

PathOver₅ _ idp c₁ c₂ = c₁ == c₂

Equivalences

The following equivalences are all provable by path-induction, we do path induction on the path α from the definition above and depending on the heterogeneous equality definition we chose we might be need other path induction. The convention for the equivalences is PathOverᵢ-≃-PathOverⱼ to denote the evidence of the equivalence between the type PathOverᵢ and PathOverⱼ.

Let us prove the equivalence between the types PathOver₁ and PathOver₂. The other equivalences are proved in a similar way but they are available on the website of this document.

-- PathOver₁-≃-PathOver₂
module _ {ℓ} (A : Type ℓ) (C : A → Type ℓ) where

-- Outgoing functions
  PathOver₁-to-PathOver₂
    : ∀ {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂}
    → PathOver₁ C α c₁ c₂
    → PathOver₂ C α c₁ c₂

  PathOver₁-to-PathOver₂ {α = idp} idp = idp

  PathOver₂-to-PathOver₁
    : ∀ {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂}
    → PathOver₂ C α c₁ c₂
    → PathOver₁ C α c₁ c₂

  PathOver₂-to-PathOver₁ {α = idp} idp = idp

Finally, we provide the evidence of the equivalence.

-- Equivalence

  PathOver₁-≃-PathOver₂ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂}
        → PathOver₁ C α c₁ c₂ ≃ PathOver₂ C α c₁ c₂
  PathOver₁-≃-PathOver₂ {α = idp}{c₁}{c₂} =
    qinv-≃
      PathOver₁-to-PathOver₂
      (PathOver₂-to-PathOver₁
        , PathOver₁~PathOver₂ , PathOver₂~PathOver₁)
    where
      PathOver₁~PathOver₂ : (p : PathOver₂ C idp c₁ c₂)
          → PathOver₁-to-PathOver₂ (PathOver₂-to-PathOver₁ p) == p
      PathOver₁~PathOver₂ idp = idp

      PathOver₂~PathOver₁ : (p : PathOver₁ C idp c₁ c₂)
          → PathOver₂-to-PathOver₁ (PathOver₁-to-PathOver₂ p) == p
      PathOver₂~PathOver₁ idp = idp

-- Other equivalences:
-- PathOver₂-≃-PathOver₃, PathOver₃-≃-PathOver₄, PathOver₄-≃-PathOver₅, PathOver₁-≃-PathOver₁

-- PathOver₂-≃-PathOver₃
module _ {ℓ} (A : Type ℓ) (C : A → Type ℓ) where

  PathOver₂-to-PathOver₃ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂}
         → PathOver₂ C α c₁ c₂
         → PathOver₃ C α c₁ c₂
  PathOver₂-to-PathOver₃ {α = idp} idp = idp

  PathOver₃-to-PathOver₂ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂}
         → PathOver₃ C α c₁ c₂
         → PathOver₂ C α c₁ c₂
  PathOver₃-to-PathOver₂ {α = idp} idp = idp

  PathOver₂-≃-PathOver₃ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂}
        → PathOver₂ C α c₁ c₂ ≃ PathOver₃ C α c₁ c₂
  PathOver₂-≃-PathOver₃ {α = idp}{c₁}{c₂} =
    qinv-≃
      PathOver₂-to-PathOver₃
      (PathOver₃-to-PathOver₂
        , PathOver₂~PathOver₃ , PathOver₃~PathOver₂)
    where
      PathOver₂~PathOver₃ : (p : PathOver₃ C idp c₁ c₂)
          → PathOver₂-to-PathOver₃ (PathOver₃-to-PathOver₂ p) == p
      PathOver₂~PathOver₃ idp = idp

      PathOver₃~PathOver₂ : (p : PathOver₂ C idp c₁ c₂)
          → PathOver₃-to-PathOver₂ (PathOver₂-to-PathOver₃ p) == p
      PathOver₃~PathOver₂ idp = idp

-- PathOver₃-≃-PathOver₄
module _ {ℓ} (A : Type ℓ) (C : A → Type ℓ) where

  PathOver₃-to-PathOver₄ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂}
         → PathOver₃ C α c₁ c₂
         → PathOver₄ C α c₁ c₂
  PathOver₃-to-PathOver₄ {α = idp} idp = idp

  PathOver₄-to-PathOver₃ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂}
         → PathOver₄ C α c₁ c₂
         → PathOver₃ C α c₁ c₂
  PathOver₄-to-PathOver₃ {α = idp} idp = idp

  PathOver₃-≃-PathOver₄ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂}
        → PathOver₃ C α c₁ c₂ ≃ PathOver₄ C α c₁ c₂
  PathOver₃-≃-PathOver₄ {α = idp}{c₁}{c₂} =
    qinv-≃
      PathOver₃-to-PathOver₄
      (PathOver₄-to-PathOver₃
        , PathOver₃~PathOver₄ , PathOver₄~PathOver₃)
    where
      PathOver₃~PathOver₄ : (p : PathOver₄ C idp c₁ c₂)
          → PathOver₃-to-PathOver₄ (PathOver₄-to-PathOver₃ p) == p
      PathOver₃~PathOver₄ idp = idp

      PathOver₄~PathOver₃ : (p : PathOver₃ C idp c₁ c₂)
          → PathOver₄-to-PathOver₃ (PathOver₃-to-PathOver₄ p) == p
      PathOver₄~PathOver₃ idp = idp

-- PathOver₄-≃-PathOver₅

module _ {ℓ} (A : Type ℓ) (C : A → Type ℓ) where

  PathOver₄-to-PathOver₅ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂}
         → PathOver₄ C α c₁ c₂
         → PathOver₅ C α c₁ c₂
  PathOver₄-to-PathOver₅ {α = idp} idp = idp

  PathOver₅-to-PathOver₄ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂}
         → PathOver₅ C α c₁ c₂
         → PathOver₄ C α c₁ c₂
  PathOver₅-to-PathOver₄ {α = idp} idp = idp

  PathOver₄-≃-PathOver₅ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂}
        → PathOver₄ C α c₁ c₂ ≃ PathOver₅ C α c₁ c₂
  PathOver₄-≃-PathOver₅ {α = idp}{c₁}{c₂} =
    qinv-≃
      PathOver₄-to-PathOver₅
      (PathOver₅-to-PathOver₄
        , PathOver₄~PathOver₅ , PathOver₅~PathOver₄)
    where
      PathOver₄~PathOver₅ : (p : PathOver₅ C idp c₁ c₂)
          → PathOver₄-to-PathOver₅ (PathOver₅-to-PathOver₄ p) == p
      PathOver₄~PathOver₅ idp = idp

      PathOver₅~PathOver₄ : (p : PathOver₄ C idp c₁ c₂)
          → PathOver₅-to-PathOver₄ (PathOver₄-to-PathOver₅ p) == p
      PathOver₅~PathOver₄ idp = idp

-- PathOver₅-≃-PathOver₁
module _ {ℓ} (A : Type ℓ) (C : A → Type ℓ) where

  PathOver₅-to-PathOver₁ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂}
         → PathOver₅ C α c₁ c₂
         → PathOver₁ C α c₁ c₂
  PathOver₅-to-PathOver₁ {α = idp} idp = idp

  PathOver₁-to-PathOver₅ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂}
         → PathOver₁ C α c₁ c₂
         → PathOver₅ C α c₁ c₂
  PathOver₁-to-PathOver₅ {α = idp} idp = idp

  PathOver₅-≃-PathOver₁ : {a₁ a₂ : A} {α : a₁ == a₂} {c₁ : C a₁}{c₂ : C a₂}
        → PathOver₅ C α c₁ c₂ ≃ PathOver₁ C α c₁ c₂
  PathOver₅-≃-PathOver₁ {α = idp}{c₁}{c₂} =
    qinv-≃
      PathOver₅-to-PathOver₁
      (PathOver₁-to-PathOver₅
        , PathOver₅~PathOver₁ , PathOver₁~PathOver₅)
    where
      PathOver₅~PathOver₁ : (p : PathOver₁ C idp c₁ c₂)
          → PathOver₅-to-PathOver₁ (PathOver₁-to-PathOver₅ p) == p
      PathOver₅~PathOver₁ idp = idp

      PathOver₁~PathOver₅ : (p : PathOver₅ C idp c₁ c₂)
          → PathOver₁-to-PathOver₅ (PathOver₅-to-PathOver₁ p) == p
      PathOver₁~PathOver₅ idp = idp

By default, we use the third definition because it is the same definition used in (Univalent Foundations Program, 2013) in Section 2.3. The syntax sugar for pathovers is used in (Brunerie et al., 2018).

PathOver = PathOver₃

infix 30 PathOver
syntax PathOver C α c₁ c₂ = c₁ == c₂ [ C ↓ α ]

Total spaces

Theorem

Let be A : Type, a path α : a₁ == a₂ of two terms a₁, a₂ : A and a type family C : A → Type. If c₁ : C a₁ and c₂ : C a₂ then the type of the pathovers between c₁ and c₁ over the path α is equivalent to the sigma type of (a₁ , c₁) == (a₂ , c₂) such that ap π₁ q == α, that is the following equivalence,

$\sum\limits_{q : (a₁ , c₁) = (a₂ , c₂)} \ (\mathsf{ap}~\mathsf{\pi_{1}}~q~= \alpha) \simeq \mathsf{PathOver}~C~\alpha~c₁~c₂.$

Proof.

module _ {ℓᵢ ℓⱼ}{A : Type ℓᵢ}{C : A → Type ℓⱼ}{a₁ a₂ : A} where

We prove this equivalence by the quasi-inverse function Σ-to-==[↓]. Therefore, we define its inverse, the function ==[↓]-to-Σ and we show the respective homotopies, Σ-to-==[↓] ∘ ==[↓]-to-Σ ~ id and ==[↓]-to-Σ ∘ Σ-to-==[↓] ~ id.

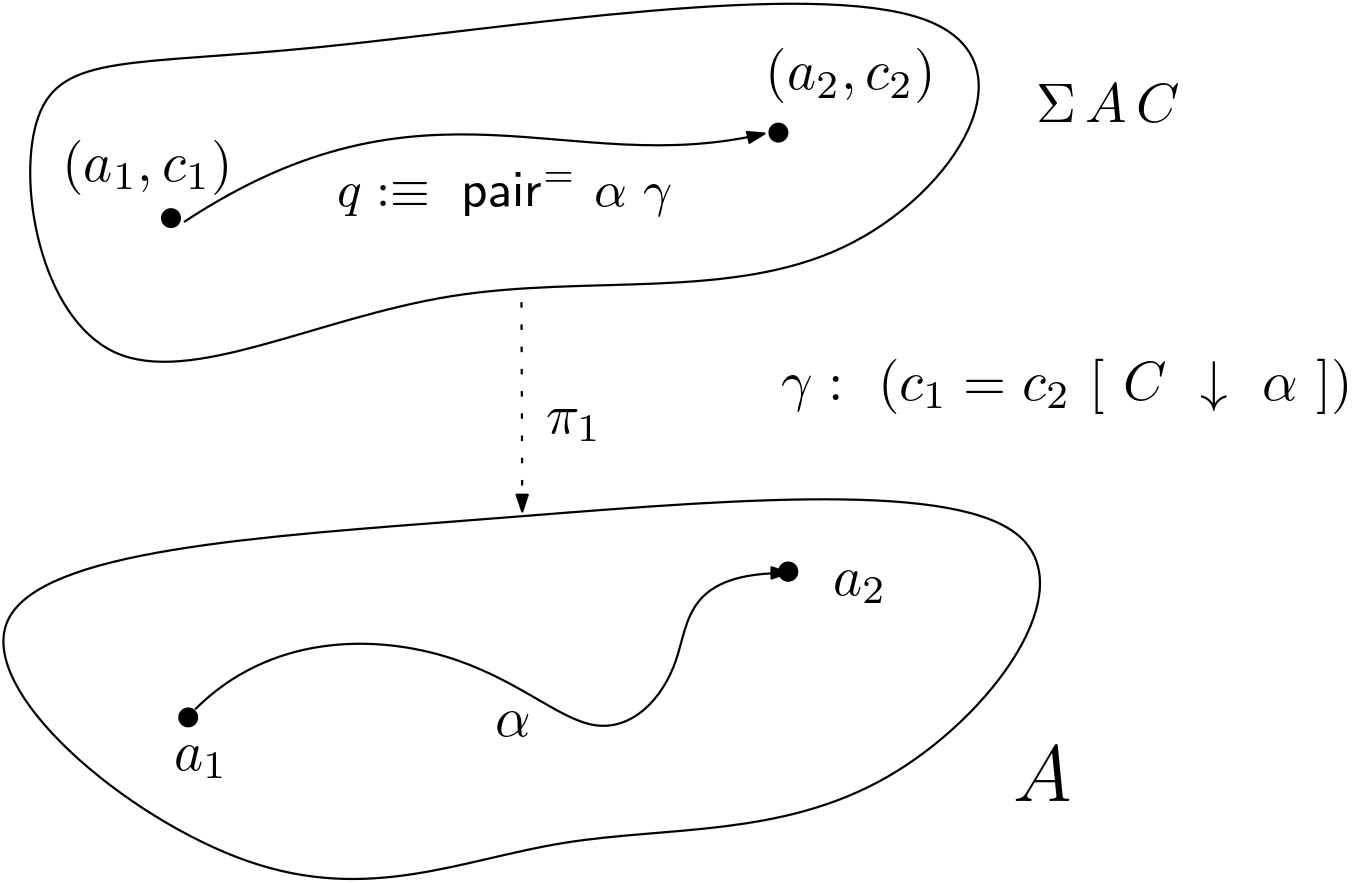path Figure 4. Pathovers and paths in the total space.

The function Σ-to-==[↓] maps a term of the sigma type in the equation above to the pathover c₁ == c₂ [ C ↓ α ]. In its construction, we use Σ-induction followed by two path-inductions on each of the its sigma components. As result, we only have to provide a term of the identity type c₁ == c₂ where c₁ and c₂ are judgementally equal, which is idp.

-- Def.
  Σ-to-==[↓] : {α : a₁ == a₂}{c₁ : C a₁}{c₂ : C a₂}
    → Σ ((a₁ , c₁) == (a₂ , c₂)) (λ q → (ap π₁ q) == α)
    → c₁ == c₂ [ C ↓  α ]
  Σ-to-==[↓] (idp , idp) = idp

The respective inverse function is ==[↓]-to-Σ, which maps terms of the pathover c₁ == c₂ [ C ↓ α ] to pairs in Σ ((a₁ , c₁) == (a₂ , c₂)) (λ q → (ap π₁ q) == α). In its construction, we use path-induction on the path α in the base space follows by the induction on the pathover γ. As result, we define this function as a pair of reflexivity proofs.

-- Def.
  ==[↓]-to-Σ : {α : a₁ == a₂}{c₁ : C a₁}{c₂ : C a₂}
    → (γ : c₁ == c₂ [ C ↓ α ])
    → Σ ((a₁ , c₁) == (a₂ , c₂)) (λ q → (ap π₁ q) == α)
  ==[↓]-to-Σ {idp} idp = (idp , idp)

Remark. We could also have defined the above function by using the pair= function which is the right-left direction in Theorem 2.7.2 in (Univalent Foundations Program, 2013) and the function ap-π₁-pair= that maps a path α in the base space and the pathover γ to a term m of type ap π₁ (pair= (α , γ)) == α. That is, ==[↓]-to-Σ α γ = (pair= α γ, m).

However, we do not get any benefit as far as we know of the latter definition against the former definition and therefore, we have preferred the former which is simpler, elegant and exploits the pattern matching of Agda as well as in the following homotopies.

-- Homotopy: Σ-to-==[↓] ∘ ==[↓]-to-Σ ~ id
  private
    H₁ : {α : a₁ == a₂}{c₁ : C a₁}{c₂ : C a₂}
       → (γ : c₁ == c₂ [ C ↓ α ])
       → Σ-to-==[↓] {α = α} (==[↓]-to-Σ γ) == γ
    H₁ {α = idp} idp = idp

-- Homotopy: ==[↓]-to-Σ ∘ Σ-to-==[↓] ∼ id
  private
    H₂ : {α : a₁ == a₂}{c₁ : C a₁}{c₂ : C a₂}
       → (pair : Σ ((a₁ , c₁) == (a₂ , c₂)) (λ q → (ap π₁ q) == α))
       → ==[↓]-to-Σ (Σ-to-==[↓] pair) == pair
    H₂ (idp , idp) = idp

Our remaining step now is to show the respective equivalence. To show that, we have used the function qinv-≃ that provides us a way to convert a quasi-inverse function into the equivalence between its domain and codomain. Since the function Σ-to-==[↓] is quasi-inverse by definition using ==[↓]-to-Σ, H₁ and H₂ hence the equivalence follows.

-- Equivalence
  private
    Σ-≃-==[↓] : {α : a₁ == a₂}{c₁ : C a₁}{c₂ : C a₂} →
      (Σ ((a₁ , c₁) == (a₂ , c₂)) (λ q → (ap π₁ q) == α))
       ≃ (c₁ == c₂ [ C ↓ α ])

    Σ-≃-==[↓] =
      qinv-≃
        Σ-to-==[↓]     -- the quasi-inverse
        ( ==[↓]-to-Σ   -- its inverse
        , H₁           -- homotopy: Σ-to-==[↓] ∘ ==[↓]-to-Σ ~ id
        , H₂           -- homotopy: ==[↓]-to-Σ ∘ Σ-to-==[↓] ∼ id
        )

In the remaining of this section, we prove some useful results about sigma types that allow us to give a shorter proof of the equivalence proved above.

Lemma 1

If $A\,,~B : U$ and $C: A → U$ and $e: B \simeq A$ , then

$\Sigma\,{A}\,C\,\simeq\,\Sigma\,B\,(C ∘ e).$

Proof.

Our context:

module Lemma₁ {ℓᵢ}{ℓⱼ}
  {A : Type ℓᵢ} {B : Type ℓᵢ} (e : B ≃ A) {C : A → Type ℓⱼ} where

We extract the functions and the homotopies from the equivalence e : B ≃ A to use them later.

-- Def.
  private
    f : B → A
    f = lemap e

    ishaef : ishae f
    ishaef = ≃-ishae e

    f⁻¹ : A → B
    f⁻¹ = ishae.g ishaef

    α : f ∘ f⁻¹ ∼ id
    α = ishae.ε ishaef

    β : f⁻¹ ∘ f  ∼ id
    β = ishae.η ishaef

    τ : (b : B) → ap f (β b) == α (f b)
    τ = ishae.τ ishaef

Now, we proceed to define the outgoing functions from $\Sigma\,{A}\,C$ to $\Sigma\,B\,(C ∘ e)$ and conversely.

-- Def.
  ΣAC-to-ΣBCf : Σ A C → Σ B (λ b → C (f b))
  ΣAC-to-ΣBCf (a , c) = f⁻¹ a , c'
    where
      c' : C (f (f⁻¹ a))
      c' = transport C ((α a) ⁻¹) c

-- Def.
  ΣBCf-to-ΣAC : Σ B (λ b → C (f b)) → Σ A C
  ΣBCf-to-ΣAC (b , c') = f b , c'

Evidence of the homotopies necessary to show the equivalence:

-- Homotopies
  private
    H₁ : ΣAC-to-ΣBCf ∘ ΣBCf-to-ΣAC ∼ id
    H₁ (b , c') = pair= (β b , patho)
      where
      c'' : C (f (f⁻¹ (f b)))
      c'' = transport C ((α (f b)) ⁻¹) c'

      -- patho : c'' == c' [ (C ∘ f) ↓ (β b)]
      patho : transport (λ x → C (f x)) (β b) c'' == c'
      patho =
        begin
          transport (λ x → C (f x)) (β b) c''
            ==⟨ transport-family (β b) c'' ⟩
          transport C (ap f (β b)) c''
            ==⟨ ap (λ γ → transport C γ c'') (τ b) ⟩
          transport C (α (f b)) c''
            ==⟨ transport-comp-h ((α (f b)) ⁻¹) (α (f b)) c' ⟩
          transport C ( ((α (f b)) ⁻¹) · α (f b)) c'
            ==⟨ ap (λ γ → transport C γ c') (·-linv (α (f b))) ⟩
          transport C idp c'
            ==⟨⟩
          c'
        ∎

  private
    H₂ : ΣBCf-to-ΣAC ∘ ΣAC-to-ΣBCf ∼ id
    H₂ (a , c) = pair= (α a , patho)
      where
      patho : transport C (α a) (transport C ((α a) ⁻¹) c) == c
      patho =
        begin
          transport C (α a) (transport C ((α a) ⁻¹) c)
            ==⟨ transport-comp-h (((α a) ⁻¹)) (α a) c ⟩
          transport C ( ((α a) ⁻¹) · (α a) ) c
            ==⟨ ap (λ γ → transport C γ c) (·-linv (α a)) ⟩
          transport C idp c
            ==⟨⟩
          c
        ∎

Finally, we now are able to prove the equivalence using the terms defined above.

-- Equivalence
  lemma₁ :  Σ A C ≃ Σ B (λ b → C (f b))
  lemma₁ = qinv-≃
            ΣAC-to-ΣBCf    -- the quasi-inverse
            ( ΣBCf-to-ΣAC  -- its inverse
            , H₁           -- ΣAC-to-ΣBCf ∘ ΣBCf-to-ΣAC ∼ id
            , H₂           -- ΣBCf-to-ΣAC ∘ ΣAC-to-ΣBCf ∼ id
            )

open Lemma₁ public

Lemma 2

If $A: U$ and $C: A → U$ and $a: A$ then

$\Sigma_{(w\,:\,\Sigma\,A\,C)}\ (\mathsf{\pi_{1}}~w~=_{A}~a)\,\simeq\,C~a.$

Proof.

module Lemma₂ {ℓ} {A : Type ℓ}{C : A → Type ℓ}(a : A) where

  ΣΣ-to-C : Σ (Σ A C) (λ w → π₁ w == a) → C a
  ΣΣ-to-C ((a , c) , p) = transport C p c

  C-to-ΣΣ : C a → Σ (Σ A C) (λ w → π₁ w == a)
  C-to-ΣΣ c = (a , c) , idp

  private
    H₁ : ΣΣ-to-C ∘ C-to-ΣΣ ∼ id
    H₁ c = idp

    H₂ : C-to-ΣΣ ∘ ΣΣ-to-C ∼ id
    H₂ ((a' , c) , p) = pair= (paireq , patho)
      where
        c' : transport C (inv p) (transport C p c) == c
        c' = begin
            transport C (inv p) (transport C p c)
              ==⟨ transport-comp-h p ((inv p)) c ⟩
            transport C (p ·  (inv p)) c
              ==⟨ ap (λ γ → transport C γ c) (·-rinv p) ⟩
            transport C idp c
              ==⟨⟩
            c
          ∎

        paireq : a , transport C p c ==  a' , c
        paireq = pair= (inv p , c')

        patho : transport (λ w → π₁ w == a) paireq idp == p
        patho
          = begin
            transport (λ w → π₁ w == ((λ _ → a) w)) paireq idp
              ==⟨ transport-eq-fun π₁ (λ _ → a) paireq idp ⟩
            inv (ap π₁ paireq) · idp · ap (λ _ → a) paireq
              ==⟨ ap (λ γ → inv (ap π₁ paireq) · idp · γ) (ap-const paireq) ⟩
            inv (ap π₁ paireq) · idp  · idp
              ==⟨ ·-runit-infer ⟩
            inv (ap π₁ paireq) · idp
              ==⟨ ·-runit-infer ⟩
            inv (ap π₁ paireq)
              ==⟨ ap (λ p → inv  p) (ap-π₁-pair= (inv p) c') ⟩
            inv (inv p)
              ==⟨ involution ⟩
             p
            ∎

  lemma₂ : Σ (Σ A C) (λ w → π₁ w == a) ≃ C a
  lemma₂ = qinv-≃ ΣΣ-to-C (C-to-ΣΣ , H₁ , H₂)

open Lemma₂ public

Lemma 3

If $A : U$ and for two type families $C,\ D: A → U$ . If we have $e :\Pi\,(a : A)~C\,a \simeq D~a$ , then

$\Sigma\,A\,C~\simeq~\Sigma\,A\,D.$

Proof.

module Lemma₃ {ℓ} {A : Type ℓ}{C : A → Type ℓ}{D : A → Type ℓ}
    (e : (a : A) → C a ≃ D a) where

  private
    f : (a : A) → C a → D a
    f a = lemap (e a)

    f⁻¹ : (a : A) → D a → C a
    f⁻¹ a = remap (e a)

    α : (a : A) → (f a) ∘ (f⁻¹ a) ∼ id
    α a x = lrmap-inverse (e a)

    β : (a : A) → (f⁻¹ a) ∘ (f a) ∼ id
    β a x = rlmap-inverse (e a)

    ΣAC-to-ΣAD :  Σ A C → Σ A D
    ΣAC-to-ΣAD (a , c) = (a , (f a) c)

    ΣAD-to-ΣAC :  Σ A D → Σ A C
    ΣAD-to-ΣAC (a , d) = (a , (f⁻¹ a) d)

    H₁ : ΣAC-to-ΣAD ∘ ΣAD-to-ΣAC ∼ id
    H₁ (a , d) = pair= (idp , α a d)

    H₂ : ΣAD-to-ΣAC ∘ ΣAC-to-ΣAD ∼ id
    H₂ (a , c) = pair= (idp  , β a c)

  lemma₃ : Σ A C ≃ Σ A D
  lemma₃ = qinv-≃ ΣAC-to-ΣAD (ΣAD-to-ΣAC , H₁ , H₂)

open Lemma₃ public

Alternative proof

Let us recall the equivalence.

$\sum\limits_{q\,:\,(a₁ , c₁) = (a₂ , c₂)} \ (\mathsf{ap}~\mathsf{\pi_{1}}~q~= \alpha) \simeq \mathsf{PathOver}~C~\alpha~c₁~c₂.$

where $a₁, a₂ : A$ , $c₁ : C~a₁$ , $c₂ : C~a₂$ and $\alpha : a₁ = a₂$ .

Using the previous lemmas, the following is an alternative proof of the theorem Σ-≃-==[↓].

Proof.

Our context for this proof:

module _ {ℓ}
  {A : Type ℓ}
  {C : A → Type ℓ}
  {a₁ a₂ : A}
  (α : a₁ == a₂)
  {c₁ : C a₁}
  {c₂ : C a₂} where

-- Theorem.
  private

    Σ-≃-==[↓] :
      Σ ((a₁ , c₁) == ( a₂ , c₂)) (λ q → ap π₁ q == α) ≃ PathOver C α c₁ c₂

    Σ-≃-==[↓] =
      begin≃
        Σ ((a₁ , c₁) == ( a₂ , c₂)) (λ q → ap π₁ q == α)
          ≃⟨ lemma₁ pair=Equiv ⟩
        Σ (Σ (a₁ == a₂) (λ β → transport C β c₁ == c₂)) (λ γ → ap π₁ (pair= γ) == α)
          ≃⟨ lemma₃ (ap-π₁-pair=Equiv α) ⟩
        Σ (Σ (a₁ == a₂) (λ β → transport C β c₁ == c₂)) (λ γ → π₁ γ == α)
          ≃⟨ lemma₂ α ⟩
        transport C α c₁ == c₂
          ≃⟨⟩
        PathOver C α c₁ c₂
      ≃∎

Agda Libraries

We based on the following Agda libraries.

Pathovers: https://github.com/HoTT/HoTT-Agda/.
Basic homotopy type theory in Agda: agda-hott.

Brunerie, G., Hou (Favonia), K.-B., Cavallo, E., Finster, E., Cockx, J., Sattler, C., … Others. (2018). Homotopy Type Theory in Agda. Retrieved from https://github.com/HoTT/HoTT-Agda
Licata, D. R., & Brunerie, G. (2015). A cubical approach to synthetic homotopy theory. Proceedings - Symposium on Logic in Computer Science, 2015-July, 92–103. https://doi.org/10.1109/LICS.2015.19
Univalent Foundations Program, T. (2013). Homotopy Type Theory: Univalent Foundations of Mathematics. Institute for Advanced Study. Retrieved from http://saunders.phil.cmu.edu/book/hott-online.pdf

Citation

If you want to cite the content of this post, we suggest to use the following latex bibtex entry. This is generated automatically.

.agda .lagda Edit History Print Cite Send Mail

Blog

Pathovers

Pathovers

Introduction

Homogeneous equality

Heterogeneous equality

Equivalences

Paths in the total space

Equivalences

Total spaces

Theorem

Lemma 1

Lemma 2

Lemma 3

Alternative proof

Agda Libraries

Citation